【题目】某中学为了了解全校学生的上网情况,在全校采用随机抽样的方法抽取了40名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
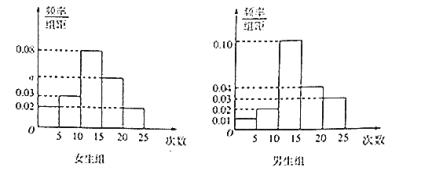
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)在抽取的40名学生中,从月上网次数不少于20次的学生中随机抽取3人 ,并用![]() 表示其中男生的人数,求
表示其中男生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)0.05;(2)详见解析.
【解析】
试题分析:(1)直接由频率分布直方图即可计算出![]() 的值即可;(2)首先求出在抽取的女生中,月上网次数不少于20次的学生频率和学生人数和在抽取的男生中,月上网次数不少于20次的学生频率和学生人数,然后确定随机变量
的值即可;(2)首先求出在抽取的女生中,月上网次数不少于20次的学生频率和学生人数和在抽取的男生中,月上网次数不少于20次的学生频率和学生人数,然后确定随机变量![]() 的所有可能取值,再利用古典概型的计算公式分别求出各自的概率并列出其分布列,最后计算出其数学期望即可.
的所有可能取值,再利用古典概型的计算公式分别求出各自的概率并列出其分布列,最后计算出其数学期望即可.
试题解析:(Ⅰ)![]() .
.
(Ⅱ)在抽取的女生中,月上网次数不少于20次的学生频率为0.02×5=0.1,学生人数为0.1×20=2人.同理,在抽取的男生中,月上网次数不少于20次的学生人数为(0.03×5)×20=3人.
故![]() 的可能取值为1,2,3.则
的可能取值为1,2,3.则![]() ,
,![]() ,
,![]() .
.
所以![]() 的分布列为:
的分布列为:

所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”。根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是 ( )
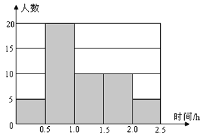
A. 甲地:总体均值为3,中位数为4
B. 乙地:总体均值为1,总体方差大于0
C. 丙地:中位数为2,众数为3
D. 丁地:总体均值为2,总体方差为3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 ,
, 时,求函数
时,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;(2)设
 ,且对任意的
,且对任意的 ,
, ,试比较
,试比较 与
与 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知p:
 ,
, ,q:
,q: ,
, ,
,(1)若q是真命题,求m的范围;
(2)若
 为真,求实数m的取值范围
为真,求实数m的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 .
.(1)判断直线
 与圆C的位置关系;
与圆C的位置关系;(2)若定点P(1,1)分弦AB为
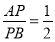 ,求此时直线
,求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:①球的半径是球面上任意一点与球心的连线;②球的直径是球面上任意两点的连线;③用一个平面截一个球面,得到的是一个圆;④球常用表示球心的字母表示.
其中说法正确的是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )
A. 792 B. 693 C. 594 D. 495
相关试题

