【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)的解析式;
(3)若x∈A,f(x)∈[﹣7,3],求区间A.
参考答案:
【答案】
(1)解:∵f(x)是奇函数,
∴f(3)+f(﹣1)=f(3)﹣f(1)=23﹣1﹣2+1=6;
(2)解:设x<0,则﹣x>0,∴f(﹣x)=2﹣x﹣1,
∵f(x)为奇函数,∴f(x)=﹣f(﹣x)=﹣2﹣x+1,
∴ ![]() ;
;
(3)解:作出函数f(x)的图象,如图所示:
根据函数图象可得f(x)在R上单调递增,
当x<0时,﹣7≤﹣2﹣x+1<0,解得﹣3≤x<0;
当x≥0时,0≤2x﹣1≤3,解得0≤x≤2;
∴区间A为[﹣3,2].
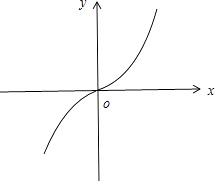
【解析】(1)根据奇函数的性质代入已知式子可求;(2)设x<0,则﹣x>0,易求f(﹣x),根据奇函数性质可得f(x)与f(﹣x)的关系;(3)作出f(x)的图象,由图象可知f(x)单调递增,由f(x)=﹣7及f(x)=3可求得相应的x值,结合图象可求得A;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|x2﹣5x﹣6<0},集合B={x|6x2﹣5x+1≥0},集合
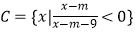
(1)求A∩B;
(2)若A∪C=C,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
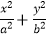 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ 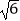 =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线L:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣ ,求证:△AOB的面积为定值.
,求证:△AOB的面积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  分别为等差数列和等比数列,
分别为等差数列和等比数列,  ,
,  的前
的前 项和为
项和为 .函数
.函数 的导函数是
的导函数是 ,有
,有 ,且
,且 是函数
是函数 的零点.
的零点.(1)求
 的值;
的值;(2)若数列
 公差为
公差为 ,且点
,且点 ,当
,当 时所有点都在指数函数
时所有点都在指数函数 的图象上.
的图象上.请你求出
 解析式,并证明:
解析式,并证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为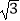 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 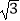 ,求直线l的方程.
,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
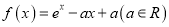 .
.(1)当
 时,求
时,求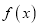 的单调区间;
的单调区间;(2)若
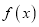 的图象与
的图象与 轴交于
轴交于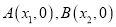 两点,起
两点,起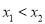 ,求
,求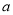 的取值范围;
的取值范围;(3)令
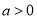 ,
, 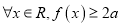 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C1:
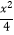 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,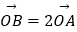 ,求直线AB的方程.
,求直线AB的方程.
相关试题

