【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为 ![]() 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 ![]() ,求直线l的方程.
,求直线l的方程.
参考答案:
【答案】
(1)解:由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),
则λ(x+y﹣4)+(3x﹣y)=0,
∵λ∈R,
∴ ![]() ,
,
解的 ![]() ,
,
∴直线l所经过的定点P的坐标(1,3)
(2)解:∵点A(2,0),点B(﹣2,0),定点P的坐标(1,3);
∴kPA= ![]() =﹣3,kPB=
=﹣3,kPB= ![]() =1,
=1,
∵直线l与线段AB有公共点,
当λ=1时,直线x=1,与线段AB有公共点,
当λ≠1时,直线l的斜率k= ![]() ,
,
∴ ![]() ≥1或
≥1或 ![]() ≤﹣3,
≤﹣3,
解的﹣1≤λ<1,或1<λ≤3,
综上所述:λ的取值范围为[﹣1,3]
(3)解:分别过A,B且斜率为 ![]() 的两条平行直线,分别为y=
的两条平行直线,分别为y= ![]() x+2
x+2 ![]() ,y=
,y= ![]() x﹣2
x﹣2 ![]() ,
,
由(1)知,l恒过点(1,3),
当斜率存在时,设直线l为y﹣3=k(x﹣1),由图象易知,直线l的倾斜角为30°,即k= ![]() ,
,
∴过点p的直线l为y﹣3= ![]() (x﹣1),即
(x﹣1),即 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0.
=0.
当直线l的斜率不存在时,由(1)可知直线过定点(1,3),则直线方程为x=1,
令x=1,可知y1=3 ![]() ,y2=﹣
,y2=﹣ ![]() ,|y1﹣y2|=4
,|y1﹣y2|=4 ![]() ,符合题意,
,符合题意,
综上所述:直线l的方程为x=1或 ![]() x﹣3y+9﹣
x﹣3y+9﹣ ![]() =0
=0
【解析】(1)由题意,(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R),由此可得方程组,从而可求定点的坐标;(2)求出A,B与定点的斜率,即可得到λ的取值范围;(3)先求出过A,B且斜率为 ![]() 的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
的两条平行直线,再分直线l的斜率存在和不存在两种情况讨论即可.
【考点精析】解答此题的关键在于理解一般式方程的相关知识,掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
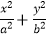 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为  ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+ 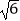 =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线L:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣ ,求证:△AOB的面积为定值.
,求证:△AOB的面积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  分别为等差数列和等比数列,
分别为等差数列和等比数列,  ,
,  的前
的前 项和为
项和为 .函数
.函数 的导函数是
的导函数是 ,有
,有 ,且
,且 是函数
是函数 的零点.
的零点.(1)求
 的值;
的值;(2)若数列
 公差为
公差为 ,且点
,且点 ,当
,当 时所有点都在指数函数
时所有点都在指数函数 的图象上.
的图象上.请你求出
 解析式,并证明:
解析式,并证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣1.
(1)求f(3)+f(﹣1);
(2)求f(x)的解析式;
(3)若x∈A,f(x)∈[﹣7,3],求区间A. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
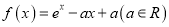 .
.(1)当
 时,求
时,求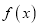 的单调区间;
的单调区间;(2)若
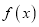 的图象与
的图象与 轴交于
轴交于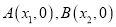 两点,起
两点,起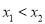 ,求
,求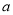 的取值范围;
的取值范围;(3)令
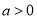 ,
, 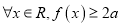 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C1:
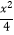 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,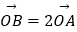 ,求直线AB的方程.
,求直线AB的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》有“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金箠,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”根据上题的已知条件,若金箠由粗到细是依次等量减小的,则正中间一尺的重量为________.
相关试题

