【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积为S= ![]() bccosA.
bccosA.
(1)求角A的大小;
(2)若c=8,点D在AC边上,且CD=2,cos∠ADB=﹣ ![]() ,求a的值.
,求a的值.
参考答案:
【答案】
(1)解:在△ABC中, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴tanA=1,∵0<A<π,∴ ![]()
(2)解:在△ABD中,∵ ![]() ,∴
,∴ ![]() ,
,
∴由正弦定理得 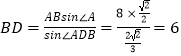 ,
,
∴在△BDC中,由余弦定理得BC2=BD2+CD2﹣2BDCDcos∠BDC=32,
∴ ![]()
【解析】(1)利用三角形的面积计算公式即可得出.(2)利用正弦定理与余弦定理即可得出.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点
的焦点 与椭圆
与椭圆 :
:  的一个焦点重合,点
的一个焦点重合,点 在抛物线上,过焦点
在抛物线上,过焦点 的直线
的直线 交抛物线于
交抛物线于 、
、 两点.
两点. (Ⅰ)求抛物线
 的方程以及
的方程以及 的值;
的值;(Ⅱ)记抛物线的准线
 与
与 轴交于点
轴交于点 ,试问是否存在常数
,试问是否存在常数 ,使得
,使得 且
且 都成立?若存在,求出实数
都成立?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=lnx,g(x)=
 +mx+
+mx+  (m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(1)求直线l的方程及实数m的值;
(2)若h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:f(a+b)﹣f(2a)< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系
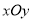 中,
中, 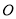 为坐标原点,曲线
为坐标原点,曲线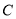 :
: 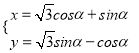 (
(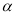 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, 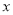 轴的正半轴为极轴,取相同单位长度的极坐标系,直线
轴的正半轴为极轴,取相同单位长度的极坐标系,直线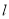 :
: 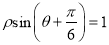 .
.(Ⅰ)求曲线
 的普通方程和直线
的普通方程和直线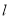 的直角坐标方程;
的直角坐标方程;(Ⅱ)曲线
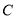 上恰好存在三个不同的点到直线
上恰好存在三个不同的点到直线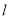 的距离相等,分别求出这三个点的极坐标.
的距离相等,分别求出这三个点的极坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体中,四边形
 为菱形,对角线
为菱形,对角线 与
与 的交点为
的交点为 ,四边形
,四边形 为梯形,
为梯形,  .
.
(Ⅰ)若
 ,求证:
,求证:  平面
平面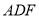 ;
;(Ⅱ)求证:平面
 平面
平面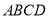 ;
;(Ⅲ)若
 ,
,  ,
,  ,求
,求 与平面
与平面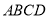 所成角.
所成角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A=[a﹣3,a],函数
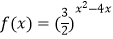 (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不过第二象限的直线l:ax﹣y﹣4=0与圆x2+(y﹣1)2=5相切.
(1)求直线l的方程;
(2)若直线l1过点(3,﹣1)且与直线l平行,直线l2与直线l1关于直线y=1对称,求直线l2的方程.
相关试题

