【题目】已知不过第二象限的直线l:ax﹣y﹣4=0与圆x2+(y﹣1)2=5相切.
(1)求直线l的方程;
(2)若直线l1过点(3,﹣1)且与直线l平行,直线l2与直线l1关于直线y=1对称,求直线l2的方程.
参考答案:
【答案】
(1)解:∵直线l与圆x2+(y﹣1)2=5相切,∴ ![]() ,
,
∵直线l不过第二象限,∴a=2,
∴直线l的方程为2x﹣y﹣4=0
(2)解:∵直线l1过点(3,﹣1)且与直线l平行,
∴直线l1的方程为2x﹣y+b=0,
∵直线l1过点(3,﹣1),∴b=﹣7,
则直线l1的方程为2x﹣y﹣7=0,
∵直线l2与l1关于y=1对称,∴直线l2的斜率为﹣2,且过点(4,1),
∴直线l2的斜率为y﹣1=﹣2(x﹣4),即化简得2x+y﹣9=0
【解析】(1)利用直线l与圆x2+(y﹣1)2=5相切, ![]() ,结合直线l不过第二象限,求出a,即可求直线l的方程;(2)直线l1的方程为2x﹣y+b=0,直线l1过点(3,﹣1),求出b,即可求出直线l1的方程;利用直线l2与l1关于y=1对称,求出直线的斜率,即可求直线l2的方程.
,结合直线l不过第二象限,求出a,即可求直线l的方程;(2)直线l1的方程为2x﹣y+b=0,直线l1过点(3,﹣1),求出b,即可求出直线l1的方程;利用直线l2与l1关于y=1对称,求出直线的斜率,即可求直线l2的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积为S=
 bccosA.
bccosA.
(1)求角A的大小;
(2)若c=8,点D在AC边上,且CD=2,cos∠ADB=﹣ ,求a的值.
,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在几何体中,四边形
 为菱形,对角线
为菱形,对角线 与
与 的交点为
的交点为 ,四边形
,四边形 为梯形,
为梯形,  .
.
(Ⅰ)若
 ,求证:
,求证:  平面
平面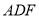 ;
;(Ⅱ)求证:平面
 平面
平面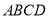 ;
;(Ⅲ)若
 ,
,  ,
,  ,求
,求 与平面
与平面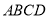 所成角.
所成角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A=[a﹣3,a],函数
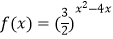 (﹣2≤x≤5)的单调减区间为集合B.
(﹣2≤x≤5)的单调减区间为集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前n项和为Sn , 且a2=3,S5=25.
(1)求数列{an}的通项公式an;
(2)设数列{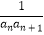 }的前n项和为Tn , 是否存在k∈N* , 使得等式2﹣2Tk=
}的前n项和为Tn , 是否存在k∈N* , 使得等式2﹣2Tk= 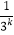 成立,若存在,求出k的值;若不存在,说明理由.
成立,若存在,求出k的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ;
;
(3)求函数g(x)=|logax﹣1|的单调区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
相关试题

