搜索
【题目】已知函数
(1)求函数
解析式；
(2)判断函数的奇偶性（给出结论即可）；
(3)若方程
参考答案：
【答案】（1）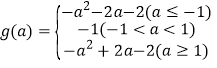
（2）偶函数（3）b<-1
【解析】
(1)将函数f(x)解析式进行化简，然后利用二次函数的图像的性质，讨论对称轴和区间的位置关系可得函数的最大值；（2）由函数图像可得函数的奇偶性；（3）根据题意可转为y=b与y=g(a)有两个不同的交点，结合图像可得b得取值范围.
(1)
=(sinxa)2-1，
∵1sinx1，∴当1<a<1时,函数的最大值为-1，
当a
1时，则当sinx=1时，函数有最大值为
，
当a
1时，当sinx=1时，函数有最大值
，所以函数f(x)的最大值
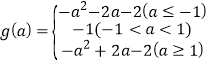
（2）函数g(x)为偶函数；
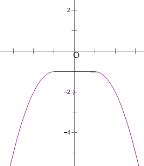
（3）若
画出函数g(a)的图像，由图像可得b<-1.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数y＝Asin(ωx＋φ)(A>0，ω>0，
)的图象过点
，图象与P点最近的一个最高点坐标为
.(1)求函数解析式；
(2)求函数的最小值，并写出相应的x值的集合；
(3)当
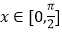时，求函数的值域. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，某几何体的三视图（单位：cm）如图所示，则该几何体的体积为（cm3）；表面积为（cm2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=lnx﹣
x2 ， g（x）= 
x2+x，m∈R，令F（x）=f（x）+g（x）． （Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若关于x的不等式F（x）≤mx﹣1恒成立，求整数m的最小值；
（Ⅲ）若m=﹣1，且正实数x1 ， x2满足F（x1）=﹣F（x2），求证：x1+x2
﹣1． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知过点
的圆
的圆心
在
轴的非负半轴上，且圆截直线
所得弦长为
．（1）求
的标准方程；（2）若过点
且斜率为
的直线
交圆于
、
两点，若
的面积为
，求直线的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】2016年汕头市开展了一场创文行动
一直以来，汕头市部分市民文明素质有待提高、环境脏乱差现象突出、交通秩序混乱、占道经营和违章搭建问题严重，为了解决这一老大难问题，汕头市政府打了一场史无前例的“创文”仗，目的是全力改善汕头市环境、卫生道路、交通各方面不文明现象，同时争夺2020年“全国文明城市”称号随着创文活动的进行，我区生活环境得到了很大的改善，但因为违法出行的三轮车减少，市民出行偶有不便有一商人从中看到商机，打算开一家汽车租赁公司，他委托一家调查公司进行市场调查，调查公司的调查结果如表：每辆车月租金定价
元
3000
3050
3100
3150
3200
3250
能出租的车辆数
辆100
99
98
97
96
95
若他打算购入汽车100辆用于租赁业务，通过调查发现租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元
由上表，他决定每辆车月租金定价满足：
为方便预测，月租金定价必须为50的整数倍；
不低于3000元；
定价必须使得公司每月至少能租10辆汽车设租赁公司每辆车月租金定价为x元时，每月能出租的汽车数量为y辆．(1)按调查数据，请将y表示为关于x的函数．
(2)当x何值时，租赁公司月收益最大？最大月收益是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】微信是现代生活中进行信息交流的重要工具.据统计，某公司200名员工中90%的人使用微信，其中每天使用微信时间在一小时以内的有60人，其余的员工每天使用微信时间在一小时以上，若将员工分成青年（年龄小于40岁）和中年（年龄不小于40岁）两个阶段，那么使用微信的人中75%是青年人.若规定：每天使用微信时间在一小时以上为经常使用微信，那么经常使用微信的员工中都是青年人.
（1）若要调查该公司使用微信的员工经常使用微信与年龄的关系，列出并完成2×2列联表：
（2）由列联表中所得数据判断，是否有99.9%的把握认为“经常使用微信与年龄有关”？
（3）采用分层抽样的方法从“经常使用微信”的人中抽取6人，从这6人中任选2人，求选出的2人，均是青年人的概率.
附：
．
相关试题
