【题目】如图,已知在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() =60°,沿
=60°,沿![]() ,
,![]() 折成三棱柱
折成三棱柱![]() .
.

(1)若![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,得到
中,得到![]() ,证得
,证得![]() 平面
平面![]() ,又由
,又由![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点证得
的中点证得![]() 平面
平面![]() ,即可证得面
,即可证得面![]() 平面
平面![]() ,利用面面平行的性质,即可得到
,利用面面平行的性质,即可得到![]() 平面
平面![]() .
.
(2)建立如图所示的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解二面角
的法向量,利用向量的夹角公式,即可求解二面角![]() 的余弦值.
的余弦值.
详解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,
中,
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
由于![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,由棱柱的性质可得
的中点,由棱柱的性质可得![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)连接![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,又
,又![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .
.
建立如图所示的空间直角坐标系,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则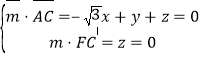 ,则
,则![]() ,令
,令![]() ,
,
得![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则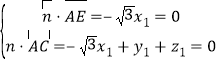 ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设![]() ,
,![]() 所成角为
所成角为![]() ,则
,则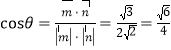 ,
,
由图可知二面角![]() 的余弦值为
的余弦值为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣a|﹣
 x,(a>0). (Ⅰ)若a=3,解关于x的不等式f(x)<0;
x,(a>0). (Ⅰ)若a=3,解关于x的不等式f(x)<0;
(Ⅱ)若对于任意的实数x,不等式f(x)﹣f(x+a)<a2+ 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中错误的是( )
A.设命题p:?x∈R,使 +x+2<0,则¬P:?x∈R,都有
+x+2<0,则¬P:?x∈R,都有 +x+2≥0
+x+2≥0
B.若x,y∈R,则“x=y”是“xy≤ 取到等号”的充要条件
取到等号”的充要条件
C.已知命题p和q,若p∧q为假命题,则命题p与q都为假命题
D.命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}共有5项,其中a1=0,a5=2,且|ai+1﹣ai|=1,i=1,2,3,4,则满足条件的不同数列的个数为( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
, .
.(1)求
 的极值;
的极值;(2) 函数
 有两个极值点
有两个极值点 ,
, ,若
,若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx,(a,b为常数,且a≠0)满足条件f(2-x)=f(x-1),且方程f(x)=x有两个相等的实根.
(1)求f(x)的解析式;
(2)设g(x)=kx+1,若F(x)=g(x)-f(x),求F(x)在[1,2]上的最小值;
(3)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]与[2m,2n],若存在,求出m,n的值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),an+1=
 , 关于下列命题:
, 关于下列命题:
①当m= 时,a5=2
时,a5=2
②若m= , 则数列{an}是周期为3的数列;
, 则数列{an}是周期为3的数列;
③对若a2=4,则m可以取3个不同的值;
④m∈Q且m∈[4,5],使得数列{an}是周期为6.
其中真命题的个数是( )
A.1
B.2
C.3
D.4
相关试题

