【题目】【2016年高考四川理数】设函数f(x)=ax2-a-lnx,其中a ∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使得![]() 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
参考答案:
【答案】(Ⅰ)当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;当
单调递减;当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增;(Ⅱ)
单调递增;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)对![]() 求导,对
求导,对![]() 进行讨论,研究
进行讨论,研究![]() 的正负,可判断函数的单调性;(Ⅱ)要证明不等式
的正负,可判断函数的单调性;(Ⅱ)要证明不等式![]() 在
在![]() 上恒成立,基本方法是设
上恒成立,基本方法是设![]() ,当
,当![]() 时,
时,![]() ,
,![]() 的解不易确定,因此结合(Ⅰ)的结论,缩小
的解不易确定,因此结合(Ⅰ)的结论,缩小![]() 的范围,设
的范围,设![]() =
=![]()
![]() ,并设
,并设![]() =
=![]() ,通过研究
,通过研究![]() 的单调性得
的单调性得![]() 时,
时,![]() ,从而
,从而![]() ,这样得出
,这样得出![]() 不合题意,又
不合题意,又![]() 时,
时,![]() 的极小值点
的极小值点![]() ,且
,且![]() ,也不合题意,从而
,也不合题意,从而![]() ,此时考虑
,此时考虑![]() 得
得![]()
![]()
![]() ,得此时
,得此时![]() 单调递增,从而有
单调递增,从而有![]() ,得出结论.
,得出结论.
试题解析:(I)![]()
![]()
![]() <0,
<0,![]() 在
在![]() 内单调递减.
内单调递减.
![]() 由
由![]() =0,有
=0,有![]() .
.
此时,当![]()
![]() 时,
时,![]() <0,
<0,![]() 单调递减;
单调递减;
当![]()
![]() 时,
时,![]() >0,
>0,![]() 单调递增.
单调递增.
(II)令![]() =
=![]() ,
,![]() =
=![]() .
.
则![]() =
=![]() .
.
而当![]() 时,
时,![]() >0,
>0,
所以![]() 在区间
在区间![]() 内单调递增.
内单调递增.
又由![]() =0,有
=0,有![]() >0,
>0,
从而当![]() 时,
时,![]() >0.
>0.
当![]() ,
,![]() 时,
时,![]() =
=![]() .
.
故当![]() >
>![]() 在区间
在区间![]() 内恒成立时,必有
内恒成立时,必有![]() .
.
当![]() 时,
时,![]() >1.
>1.
由(I)有![]() ,从而
,从而![]() ,
,
所以此时![]() >
>![]() 在区间
在区间![]() 内不恒成立.
内不恒成立.
当![]() 时,令
时,令![]() ,
,
当![]() 时,
时,![]() ,
,
因此,![]() 在区间
在区间![]() 单调递增.
单调递增.
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即 ![]() 恒成立.
恒成立.
综上,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
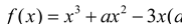 .
.(1)若函数
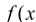 在区间
在区间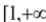 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;(2)若
 是函数
是函数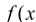 的极值点,求函数
的极值点,求函数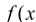 在
在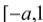 上的最大值;
上的最大值;(3)在(2)的条件下,是否存在实数
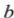 ,使得函数
,使得函数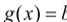 的图象与函数
的图象与函数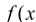 的图象恰有
的图象恰有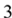 个交点?若存在,请求出
个交点?若存在,请求出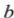 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设首项为1的正项数列{an}的前n项和为Sn,且Sn+1-3Sn=1.
(1) 求证:数列{an}为等比数列;
(2) 数列{an}是否存在一项ak,使得ak恰好可以表示为该数列中连续r(r∈N*,r≥2)项的和?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届江西省南昌市高三第一次模拟考试数学(理)】已知函数
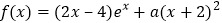 (
(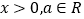 ,
,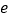 是自然对数的底数).
是自然对数的底数).(1)若
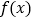 是
是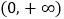 上的单调递增函数,求实数
上的单调递增函数,求实数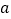 的取值范围;
的取值范围;(2)当
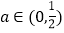 时,证明:函数
时,证明:函数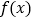 有最小值,并求函数
有最小值,并求函数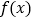 最小值的取值范围.
最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考江苏卷】已知函数
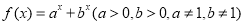 .设
.设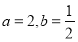 .
.(1)求方程
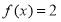 的根;
的根;(2)若对任意
 ,不等式
,不等式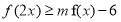 恒成立,求实数
恒成立,求实数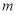 的最大值;
的最大值;(3)若
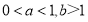 ,函数
,函数 有且只有1个零点,求
有且只有1个零点,求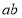 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等比数列{an}满足:|a2-a3|=10,a1a2a3=125.
(1) 求{an}的通项公式;
(2) 求证:
 +
+ +…+
+…+ <1对任意正整数m都成立.
<1对任意正整数m都成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
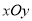 中,已知曲线
中,已知曲线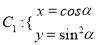 (
(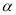 为参数),在以
为参数),在以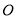 为极点,
为极点, 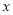 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线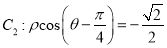 ,曲线
,曲线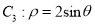 .
.(1)求曲线
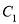 与
与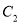 的交点
的交点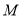 的直角坐标;
的直角坐标;(2)设点
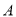 ,
, 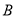 分别为曲线
分别为曲线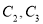 上的动点,求
上的动点,求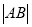 的最小值.
的最小值.
相关试题

