【题目】设首项为1的正项数列{an}的前n项和为Sn,且Sn+1-3Sn=1.
(1) 求证:数列{an}为等比数列;
(2) 数列{an}是否存在一项ak,使得ak恰好可以表示为该数列中连续r(r∈N*,r≥2)项的和?请说明理由.
参考答案:
【答案】(1) 见解析. (2) 见解析.
【解析】试题分析:(1)由![]() 可得
可得![]() ,两式相减化简可得数列{an}为等比数列;(2)假设数列
,两式相减化简可得数列{an}为等比数列;(2)假设数列![]() 中存在一项
中存在一项![]() 恰好可以表示为该数列中连续项的和,利用等比数列求和化简后,导出矛盾即可得结论.
恰好可以表示为该数列中连续项的和,利用等比数列求和化简后,导出矛盾即可得结论.
试题解析:(1)∵ Sn+1-3Sn=1,∴ n≥2时Sn-3Sn-1=1,两式相减得an+1-3an=0,即an+1=3an(n≥2).
又a1=1,S2-3S1=1,∴ a2=3,∴ n=1时an+1=3an也成立.
∴ n∈N*时![]() =3,数列{an}为等比数列.
=3,数列{an}为等比数列.
(2) 解:由(1)知an=3n-1,若数列{an}中存在一项ak,使得ak=am+am+1+am+2+…+am+r-1(m∈N*).(2)
∵ an=3n-1,∴ {an}为递增数列.
∴ ak>am+r-1,即3k-1>3m+r-2,k>m+r-1,k≥m+r.
又am+am+1+am+2+…+am+r-1=![]() <
<![]() ≤
≤![]() <3k-1=ak与ak=am+am+1+am+2+…+am+r-1相矛盾.
<3k-1=ak与ak=am+am+1+am+2+…+am+r-1相矛盾.
∴ 数列{an}不存在一项ak,使得ak恰好可以表示为该数列中连续r(r∈N*,r≥2)项的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届广东省深圳市高三下学期第一次调研考试(一模)数学理】已知函数
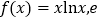 为自然对数的底数.
为自然对数的底数.(1)求曲线
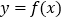 在
在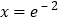 处的切线方程;
处的切线方程;(2)关于
 的不等式
的不等式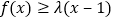 在
在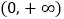 上恒成立,求实数
上恒成立,求实数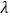 的值;
的值;(3)关于
 的方程
的方程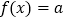 有两个实根
有两个实根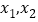 ,求证:
,求证: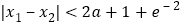 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在公差不为零的等差数列{an}中,已知a1=1,且a1,a2,a5依次成等比数列.数列{bn}满足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通项公式;
(2)设数列
 的前n项和为Sn,试比较Sn与1-
的前n项和为Sn,试比较Sn与1- 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
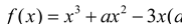 .
.(1)若函数
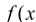 在区间
在区间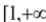 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;(2)若
 是函数
是函数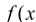 的极值点,求函数
的极值点,求函数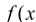 在
在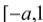 上的最大值;
上的最大值;(3)在(2)的条件下,是否存在实数
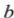 ,使得函数
,使得函数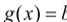 的图象与函数
的图象与函数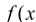 的图象恰有
的图象恰有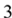 个交点?若存在,请求出
个交点?若存在,请求出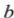 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2017届江西省南昌市高三第一次模拟考试数学(理)】已知函数
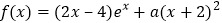 (
(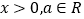 ,
,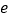 是自然对数的底数).
是自然对数的底数).(1)若
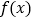 是
是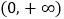 上的单调递增函数,求实数
上的单调递增函数,求实数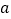 的取值范围;
的取值范围;(2)当
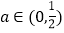 时,证明:函数
时,证明:函数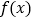 有最小值,并求函数
有最小值,并求函数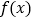 最小值的取值范围.
最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016年高考四川理数】设函数f(x)=ax2-a-lnx,其中a ∈R.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)确定a的所有可能取值,使得
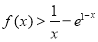 在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数). -
科目: 来源: 题型:
查看答案和解析>>【题目】【2016高考江苏卷】已知函数
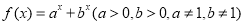 .设
.设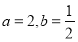 .
.(1)求方程
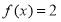 的根;
的根;(2)若对任意
 ,不等式
,不等式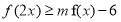 恒成立,求实数
恒成立,求实数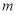 的最大值;
的最大值;(3)若
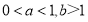 ,函数
,函数 有且只有1个零点,求
有且只有1个零点,求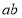 的值。
的值。
相关试题

