【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )在一个周期内的图像如图所示,其中M(
)在一个周期内的图像如图所示,其中M( ![]() ,2),N(
,2),N( ![]() ,0).
,0). 
(1)求函数f(x)的解析式;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且a= ![]() ,c=3,f(
,c=3,f( ![]() )=
)= ![]() ,求△ABC的面积.
,求△ABC的面积.
参考答案:
【答案】
(1)解:由图像可知:函数f(x)的周期T=4×( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω= ![]() =2.
=2.
又f(x)过点( ![]() ,2),
,2),
∴f( ![]() )=2sin(
)=2sin( ![]() +φ)=2,sin(
+φ)=2,sin( ![]() +φ)=1,
+φ)=1,
∵|φ|< ![]() ,
, ![]() +φ∈(﹣
+φ∈(﹣ ![]() ,
, ![]() ),
),
∴ ![]() +φ=
+φ= ![]() ,即φ=
,即φ= ![]() .
.
∴f(x)=2sin(2x+ ![]() ).
).
(2)解:∵f( ![]() )=2sin(A+
)=2sin(A+ ![]() )=
)= ![]() ,即sin(A+
,即sin(A+ ![]() )=
)= ![]() ,
,
又A∈(0,π),A+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
∴A+ ![]() =
= ![]() ,即A=
,即A= ![]() .
.
在△ABC中,A= ![]() ,a=
,a= ![]() ,c=3,
,c=3,
由余弦定理得 a2=b2+c2﹣2bccosA,
∴13=b2+9﹣3b,即b2﹣3b﹣4=0,
解得b=4或b=﹣1(舍去).
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() =3
=3 ![]()
【解析】(1)由图像可求f(x)的周期T,由周期公式可得ω,又f(x)过点( ![]() ,2),结合|φ|<
,2),结合|φ|< ![]() ,即可求得φ的值,从而可求函数f(x)的解析式;(2)由f(
,即可求得φ的值,从而可求函数f(x)的解析式;(2)由f( ![]() )=2sin(A+
)=2sin(A+ ![]() )=
)= ![]() ,结合A∈(0,π),即可求得A的值,在△ABC中,由余弦定理得b2﹣3b﹣4=0,解得b的值,由三角形面积公式即可得解.
,结合A∈(0,π),即可求得A的值,在△ABC中,由余弦定理得b2﹣3b﹣4=0,解得b的值,由三角形面积公式即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50].
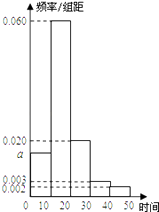
(1)求频率分布直方图中a的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人进行乒乓球决赛,比赛采取七局四胜制.现在的情形是甲胜3局,乙胜2局.若两人胜每局的概率相同,则甲获得冠军的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线 的极坐标方程为
的极坐标方程为 ,
,  .
.(Ⅰ)若直线
 与曲线
与曲线 交于不同的两点
交于不同的两点 ,
,  ,当
,当 时,求
时,求 的值;
的值;(Ⅱ)当
 时,求曲线
时,求曲线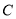 关于直线
关于直线 对称的曲线方程.
对称的曲线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,且CD=2,AB=BC=PA=1,PD=
 .
. 
(1)求三棱锥A﹣PCD的体积;
(2)问:棱PB上是否存在点E,使得PD∥平面ACE?若存在,求出 的值,并加以证明;若不存在,请说明理由.
的值,并加以证明;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣
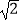 ,0),B(
,0),B( 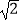 ,0),动点E满足直线EA与直线EB的斜率之积为﹣
,0),动点E满足直线EA与直线EB的斜率之积为﹣  .
.
(1)求动点E的轨迹C的方程;
(2)设过点F(1,0)的直线l1与曲线C交于点P,Q,记点P到直线l2:x=2的距离为d.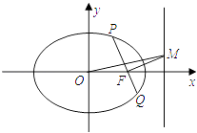
(ⅰ)求 的值;
的值;
(ⅱ)过点F作直线l1的垂线交直线l2于点M,求证:直线OM平分线段PQ. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋中共有8个球,其中3个红球、2个白球、3个黑球.若从袋中任取3个球,则所取3个球中至多有1个红球的概率是( )
A.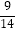
B.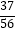
C.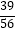
D.
相关试题

