【题目】已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)若![]() ,且a分别与
,且a分别与![]() ,
,![]() 垂直,求向量a的坐标;
垂直,求向量a的坐标;
(2)若![]() ∥
∥![]() ,且
,且![]() ,求点P的坐标.
,求点P的坐标.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)![]() =(﹣2,﹣1,3),
=(﹣2,﹣1,3),![]() =(1,﹣3,2).设
=(1,﹣3,2).设![]() =(x,y,z),由于|
=(x,y,z),由于|![]() |=
|=![]() ,且
,且![]() 分别与
分别与![]() 、
、![]() 垂直,可得
垂直,可得 ,解出即可.(2) 设
,解出即可.(2) 设![]() ,
,
![]() ,解之即得
,解之即得![]() 的值,即得
的值,即得![]() =(6,-4,-2)或
=(6,-4,-2)或![]() =(-6,4,2).再求出点P的坐标.
=(-6,4,2).再求出点P的坐标.
(1)![]() =(﹣2,﹣1,3),
=(﹣2,﹣1,3),![]() =(1,﹣3,2).
=(1,﹣3,2).
设![]() =(x,y,z),
=(x,y,z),
∵|![]() |=
|=![]() ,且
,且![]() 分别与
分别与![]() 、
、![]() 垂直,
垂直,
∴ ,
,
解得 ,或
,或 .
.
∴![]() =(1,1,1),(﹣1,﹣1,﹣1).
=(1,1,1),(﹣1,﹣1,﹣1).
(2)因为![]() ∥
∥![]() ,所以可设
,所以可设![]() .
.
因为![]() =(3,-2,-1),
=(3,-2,-1),
所以![]() =(3λ,-2λ,-λ).
=(3λ,-2λ,-λ).
又因为![]() ,
,
所以![]() ,
,
解得λ=±2.
所以![]() =(6,-4,-2)或
=(6,-4,-2)或![]() =(-6,4,2).
=(-6,4,2).
设点P的坐标为(x,y,z),则![]() =(x,y-2,z-3).
=(x,y-2,z-3).
所以 或
或
解得 或
或
故所求点P的坐标为(6,-2,1)或(-6,6,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(1,2,3),B(2,1,2),C(1,1,2),O为坐标原点,点D在直线OC上运动,则当
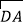 ·
·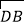 取最小值时,点D的坐标为( )
取最小值时,点D的坐标为( )A.
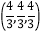 B.
B. 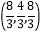
C.
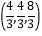 D.
D. 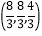
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 +k(
+k(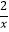 +lnx)(k为常数).
+lnx)(k为常数).
(1)当k=0时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当k≥0时,求函数f(x)的单调区间;
(3)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若
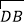 ∥
∥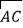 ,
,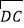 ∥
∥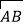 ,求点D的坐标;
,求点D的坐标;(2)问是否存在实数α,β,使得
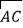 =α
=α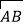 +β
+β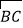 成立?若存在,求出α,β的值;若不存在,说明理由.
成立?若存在,求出α,β的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是________(填序号).
①若
 ,
, 分别是平面α,β的一个法向量,则
分别是平面α,β的一个法向量,则 ∥
∥ α∥β;
α∥β;②若
 ,
, 分别是平面α,β的一个法向量,则α⊥β
分别是平面α,β的一个法向量,则α⊥β ·
· =0;
=0;③若
 是平面α的一个法向量,
是平面α的一个法向量,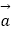 与平面α共面,则
与平面α共面,则 ·
·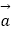 =0;
=0;④若两个平面的法向量不垂直,则这两个平面一定不垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A﹣{1,2,3,4,5,6,7,8,9),在集合A中任取三个元素,分别作为一个三位数的个位数,十位数和百位数,记这个三位数为a,现将组成a的三个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=219,则I(a)=129,D(a)=921),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,则输出b的值为( )

A.792
B.693
C.594
D.495 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥PABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC=
 AD=1.问:在棱PD上是否存在一点E,使得CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.
AD=1.问:在棱PD上是否存在一点E,使得CE∥平面PAB?若存在,求出E点的位置;若不存在,请说明理由.
相关试题

