【题目】已知函数![]() ,
,![]()
![]() .
.
(1)求函数![]() 的单调区间与极值.
的单调区间与极值.
(2)当![]() 时,是否存在
时,是否存在![]() ,使得
,使得![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
参考答案:
【答案】(1)分类讨论,详见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的定义域,接着求导,对参数
的定义域,接着求导,对参数![]() 分类讨论。
分类讨论。
(2)假设存在![]() ,使得
,使得![]() 成立,则对
成立,则对![]() ,满足
,满足![]() ,将问题转化为求
,将问题转化为求![]() 与
与![]() 。
。
解:(1)![]() ,
,
当![]() 时,
时,![]() 恒成立,即函数
恒成立,即函数![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间,所以不存在极值.
,无单调减区间,所以不存在极值.
当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,此时函数
,此时函数![]() 在
在![]() 处取得极大值,极大值为
处取得极大值,极大值为
综上,当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,无单调减区间,不存在极值.当
,无单调减区间,不存在极值.当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,极大值为
,极大值为![]() ,无极小值
,无极小值
(2)当![]() 时,假设存在
时,假设存在![]() ,使得
,使得![]() 成立,则对
成立,则对![]() ,满足
,满足![]()
由![]()
![]() 可得,
可得,
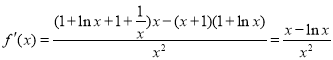 .
.
令![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
由(1)可知,①当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 的最小值是
的最小值是![]() .
.
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 的最小值是
的最小值是![]() .
.
③当![]() 时,即
时,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.又
上单调递减.又![]() ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]() .当
.当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]()
所以当![]() 时,
时,![]() 在
在![]() 上的最小值是
上的最小值是![]() ,故
,故![]() ,
,
解得![]() ,所以
,所以![]() .
.
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值是
上的最小值是![]() ,故
,故![]() ,
,
解得![]() ,所以
,所以![]() .故实数
.故实数![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
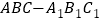 中,
中,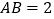 ,
,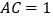 ,
,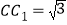 ,
,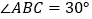 ,
,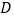 为
为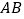 的中点.
的中点.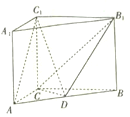
(1)证明:
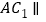 平面
平面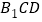 ;
;(2)求直线
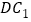 与平面
与平面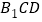 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
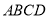 是正方形,点
是正方形,点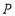 在以
在以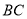 为直径的半圆弧上(
为直径的半圆弧上(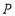 不与
不与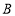 ,
,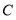 重合),
重合),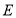 为线段
为线段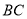 的中点,现将正方形
的中点,现将正方形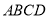 沿
沿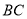 折起,使得平面
折起,使得平面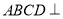 平面
平面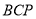 .
.
(1)证明:
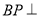 平面
平面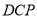 .
.(2)若
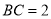 ,当三棱锥
,当三棱锥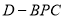 的体积最大时,求
的体积最大时,求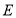 到平面
到平面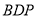 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)当
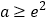 时,若存在
时,若存在 ,使得对任意的
,使得对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]:在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 ,
, 的直角坐标方程;
的直角坐标方程;(2)判断曲线
 ,
, 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知ω>0,0<φ<π,直线
 和
和 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,若将函数f(x)图象上每一点的横坐标变为原来的 倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )
倍,纵坐标变为原来的2倍,则得到的图象的函数解析式是( )A.
 B.
B.
C.y=2cos2xD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟.那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A.
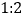 B.
B. 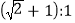 C.
C. 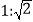 D.
D. 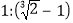
相关试题

