【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
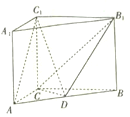
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
参考答案:
【答案】(1)见解析 (2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由矩形的性质,结合三角形中位线定理可得
,由矩形的性质,结合三角形中位线定理可得![]() ,由线面平行的判定定理可得结果;(2)先证明
,由线面平行的判定定理可得结果;(2)先证明![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,求得直线
轴建立如图所示的空间直角坐标系,求得直线![]() 的方向向量,利用向量垂直数量积为零列方程求得平面
的方向向量,利用向量垂直数量积为零列方程求得平面![]() 的法向量,由空间向量夹角余弦公式可得结果.
的法向量,由空间向量夹角余弦公式可得结果.
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,因为四边形
,因为四边形![]() 是矩形,所以点
是矩形,所以点![]() 是
是![]() 的中点,
的中点,
又点![]() 为
为![]() 的中点,所以
的中点,所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
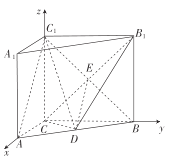
(2)由![]() ,
,![]() ,
,![]() ,可得
,可得![]() ,
,
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
则有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,
,
则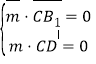 ,即
,即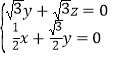 ,令
,令![]() ,得
,得![]() ,
,
所以![]()
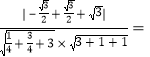
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的有( )
A.设正六棱锥的底面边长为1,侧棱长为
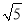 ,那么它的体积为
,那么它的体积为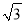
B.用斜二测法作△ABC的水平放置直观图得到边长为a的正三角形,则△ABC面积为
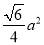
C.三个平面可以将空间分成4,6,7或者8个部分
D.已知四点不共面,则其中任意三点不共线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年是中国改革开放的第40周年,为了充分认识新形势下改革开放的时代性,某地的民调机构随机选取了该地的100名市民进行调查,将他们的年龄分成6段:
 ,并绘制了如图所示的频率分布直方图.
,并绘制了如图所示的频率分布直方图.
(1)现从年龄在
 内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用
内的人员中按分层抽样的方法抽取8人,再从这8人中随机抽取3人进行座谈,用 表示年龄在
表示年龄在 内的人数,求
内的人数,求 的分布列和数学期望;
的分布列和数学期望;(2)若用样本的频率代替概率,用随机抽样的方法从该地抽取20名市民进行调查,其中有
 名市民的年龄在
名市民的年龄在 的概率为
的概率为 .当
.当 最大时,求
最大时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量低于20mg的驾驶员可以驾驶汽车,酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶汽车?( )(参考数据:lg0.2≈﹣0.7,1g0.3≈﹣0.5,1g0.7≈﹣0.15,1g0.8≈﹣0.1)
A.1B.3C.5D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
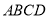 是正方形,点
是正方形,点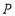 在以
在以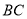 为直径的半圆弧上(
为直径的半圆弧上(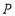 不与
不与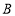 ,
,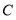 重合),
重合),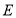 为线段
为线段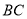 的中点,现将正方形
的中点,现将正方形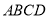 沿
沿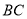 折起,使得平面
折起,使得平面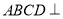 平面
平面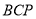 .
.
(1)证明:
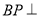 平面
平面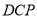 .
.(2)若
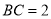 ,当三棱锥
,当三棱锥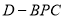 的体积最大时,求
的体积最大时,求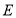 到平面
到平面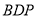 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)当
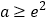 时,若存在
时,若存在 ,使得对任意的
,使得对任意的 ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
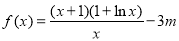 ,
,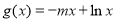
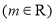 .
.(1)求函数
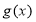 的单调区间与极值.
的单调区间与极值.(2)当
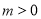 时,是否存在
时,是否存在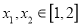 ,使得
,使得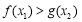 成立?若存在,求实数
成立?若存在,求实数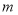 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
相关试题

