【题目】如图,棱形![]() 的边长为6,
的边长为6, ![]() ,
,![]() .将棱形
.将棱形![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点, ![]() .
.
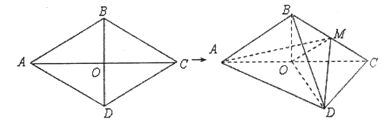
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)求证:![]() 平面
平面![]() ,这是证明线面平行问题,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题注意到
,这是证明线面平行问题,证明线面平行,即证线线平行,可利用三角形的中位线,或平行四边形的对边平行,本题注意到![]() 是
是![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 的中点,因此由三角形的中位线可得,
的中点,因此由三角形的中位线可得,![]() ,从而可得
,从而可得![]() 平面
平面![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积,由已知
的体积,由已知![]() ,由题意
,由题意![]() ,可得
,可得![]() ,从而得
,从而得![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() ,因此把求三棱锥
,因此把求三棱锥![]() 的体积,转化为求三棱锥
的体积,转化为求三棱锥![]() 的体积,因为高
的体积,因为高![]() ,求出
,求出![]() 的面积即可求出三棱锥
的面积即可求出三棱锥![]() 的体积.
的体积.
试题解析:(1)证明:因为点![]() 是菱形
是菱形![]() 的对角线的交点,
的对角线的交点,
所以![]() 是
是![]() 的中点.又点
的中点.又点![]() 是棱
是棱![]() 的中点,
的中点,
所以![]() 是
是![]() 的中位线,
的中位线,![]() . 2分
. 2分
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 4分
, 4分
所以![]() 平面
平面![]() . 6分
. 6分
(2)三棱锥![]() 的体积等于三棱锥
的体积等于三棱锥![]() 的体积. 7分
的体积. 7分
由题意,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() . 8分
. 8分
又因为菱形![]() ,所以
,所以![]() . 9分
. 9分
因为![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() 10分
10分
所以![]() 为三棱锥
为三棱锥![]() 的高. 11分
的高. 11分
![]() 的面积为
的面积为![]()
![]() , 13分
, 13分
所求体积等于![]()
![]() . 14分
. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
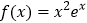 .
.(Ⅰ)求曲线
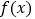 在点
在点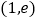 处的切线方程;
处的切线方程;(Ⅱ)若
 对
对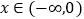 恒成立,求实数
恒成立,求实数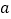 的取值范围;
的取值范围;(Ⅲ)求整数
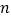 的值,使函数
的值,使函数 在区间
在区间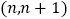 上有零点.
上有零点. -
科目: 来源: 题型:
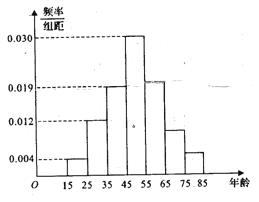
查看答案和解析>>【题目】2017年天猫五一活动结束后,某地区研究人员为了研究该地区在五一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得概率分布直方图如图所示:记年龄在
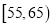 ,
, 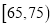 ,
, 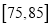 对应的小矩形的面积分别是
对应的小矩形的面积分别是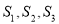 ,且
,且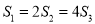 .
.
(1)以频率作为概率,若该地区五一消费超过3000元的有30000人,试估计该地区在五一活动中消费超过3000元且年龄在
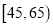 的人数;
的人数;(2)计算在五一活动中消费超过3000元的消费者的平均年龄;
(3)若按照分层抽样,从年龄在
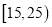 ,
, 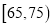 的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在
的人群中共抽取7人,再从这7人中随机抽取2人作深入调查,求至少有1人的年龄在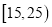 内的概率.
内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
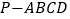 中,底面
中,底面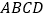 为平行四边形,
为平行四边形, 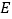 为侧棱
为侧棱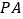 的中点.
的中点.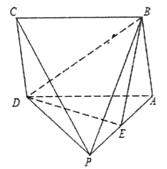
(Ⅰ)求证:
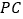 ∥平面
∥平面
(Ⅱ)若
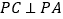 ,
,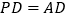 ,
,求证:平面

 平面
平面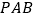
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
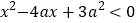 ,其中
,其中 ,命题
,命题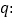 实数
实数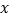 满足
满足|x-3|≤1 .
(1)若
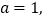 且
且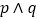 为真,求实数
为真,求实数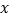 的取值范围;
的取值范围;(2)若
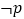 是
是
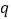 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将圆的一组
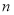 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录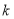 (
(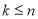 )个点的颜色,称为该圆的一个“
)个点的颜色,称为该圆的一个“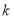 阶色序”,当且仅当两个
阶色序”,当且仅当两个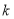 阶色序对应位置上的颜色至少有一个不相同时,称为不同的
阶色序对应位置上的颜色至少有一个不相同时,称为不同的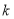 阶色序.若某国的任意两个“
阶色序.若某国的任意两个“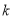 阶色序”均不相同,则称该圆为“
阶色序”均不相同,则称该圆为“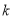 阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )A.4 B.6 C.8 D.10
-
科目: 来源: 题型:
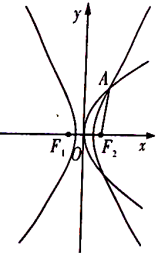
查看答案和解析>>【题目】如图,抛物线
 :
: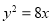 与双曲线
与双曲线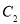 :
: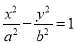 (
(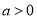 ,
,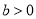 )有公共焦点
)有公共焦点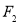 ,点
,点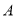 是曲线
是曲线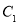 ,
,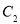 在在第一象限的交点,且
在在第一象限的交点,且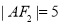 .
.
(1)求双曲线
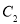 的方程;
的方程;(2)以
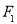 为圆心的圆
为圆心的圆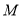 与双曲线的一条渐进线相切,圆
与双曲线的一条渐进线相切,圆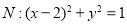 .已知点
.已知点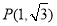 ,过点
,过点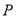 作互相垂直分别与圆
作互相垂直分别与圆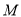 、圆
、圆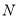 相交的直线
相交的直线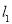 和
和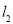 ,设
,设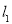 被圆
被圆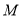 解得的弦长为
解得的弦长为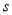 ,
,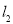 被圆
被圆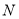 截得的弦长为
截得的弦长为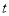 .试探索
.试探索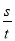 是否为定值?请说明理由.
是否为定值?请说明理由.
相关试题

