【题目】已知函数![]() .
.
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)求函数![]() 在区间
在区间![]() 上的最大值及最小值.
上的最大值及最小值.
参考答案:
【答案】(Ⅰ)![]() ,
, ![]() ;(Ⅱ)
;(Ⅱ)![]() 取得最大值
取得最大值![]() ,
, ![]() 取得最小值
取得最小值![]() .
.
【解析】试题分析:(Ⅰ)先根据两角和余弦公式、二倍角公式、配角公式将函数化为基本三角函数: ![]()
![]() ,再根据正弦函数性质求单调区间:由
,再根据正弦函数性质求单调区间:由![]() 解得
解得![]() ,最后写出区间形式(Ⅱ)先根据自变量范围
,最后写出区间形式(Ⅱ)先根据自变量范围![]() 确定基本三角函数定义区间:
确定基本三角函数定义区间:![]() ,再根据正弦函数在此区间图像确定最值:当
,再根据正弦函数在此区间图像确定最值:当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() 取得最大值1.
取得最大值1.
试题解析:(Ⅰ)![]()
![]()
![]()
![]()
![]() . ……………………………………3分
. ……………………………………3分
由![]() ,
,![]() ,得
,得![]() ,
,![]() .
.
即![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() .……………………6分
.……………………6分
(Ⅱ)由![]() 得
得![]() , ………………………………8分
, ………………………………8分
所以![]() . …………………………………………10分
. …………………………………………10分
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
当![]() 时,
时,![]() 取得最大值1. ………………………………13分
取得最大值1. ………………………………13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了300名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作
不愿意做志愿者工作
合计
男大学生
180
女大学生
45
合计
200
(Ⅰ)根据题意完成表格;
(Ⅱ)是否有
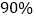 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?附:
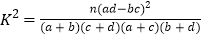 ,
,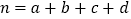
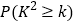
0.5
0.40
0.25
0.15
0.10
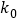
0.455
0.708
1.323
.072
2.706
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知点
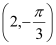 ,圆
,圆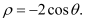
(I)在极坐标系中,以极点为原点,极轴为
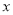 轴正半轴建立平面直角坐标系,取相同的长度单位,求圆
轴正半轴建立平面直角坐标系,取相同的长度单位,求圆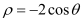 的直角坐标方程;
的直角坐标方程;(II)求点
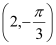 到圆
到圆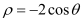 圆心的距离.
圆心的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了研究某种微生物的生长规律,需要了解环境温度
 (
(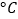 )对该微生物的活性指标
)对该微生物的活性指标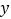 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:环境温度
 (
(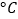 )
)1
2
3
4
5
6
7
活性指标
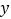
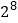
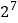
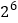
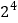
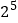
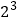
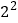
(Ⅰ)由表中数据判断
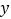 关于
关于 的关系较符合
的关系较符合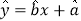 还是
还是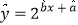 ,并求
,并求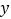 关于
关于 的回归方程(
的回归方程(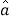 ,
,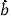 取整数);
取整数);(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于
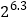 ,则环境温度应不得高于多少
,则环境温度应不得高于多少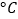 ?
?附:
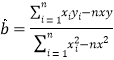 ,
,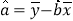
-
科目: 来源: 题型:
查看答案和解析>>【题目】随机抽取了40辆汽车在经过路段上某点是的车速(
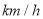 ),现将其分成六段:
),现将其分成六段: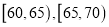 ,
,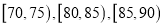 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.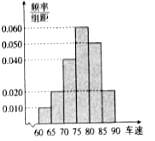
(I)现有某汽车途经该点,则其速度低于80
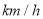 的概率约是多少?
的概率约是多少?(II)根据频率分布直方图,抽取的40辆汽车经过该点的平均速度是多少?
(III)在抽取的40辆汽车且速度在
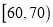 (
(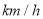 )内的汽车中任取2辆,求这2辆车车速都在
)内的汽车中任取2辆,求这2辆车车速都在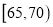 (
(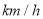 )内的概率.
)内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
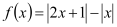 .
.(I)求证:
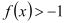 恒成立;
恒成立;(II)若存在实数
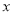 ,使得
,使得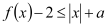 ,求实数
,求实数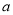 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设锐角三角形的内角
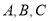 的对边分别为
的对边分别为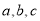 ,且
,且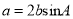 .
.(1)求
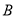 的大小;
的大小;(2)求
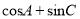 的取值范围.
的取值范围.
相关试题

