【题目】已知函数![]() ,
, ![]() (
(![]() ),设方程
),设方程![]() ,
, ![]() ,
, ![]() 的实根的个数为分别为
的实根的个数为分别为![]() 、
、![]() 、
、![]() ,则
,则![]()
A. 9 B. 13 C. 17 D. 21
参考答案:
【答案】B
【解析】由条件可在函数![]() 的值域为
的值域为![]() ,方程
,方程![]() 的根为0,
的根为0, ![]() ,
, ![]() ,所以方程
,所以方程![]() 的根为方程
的根为方程![]() 或
或![]() 或
或![]() 的根,显然方程
的根,显然方程![]() 有3个实根,
有3个实根, ![]() 与
与![]() 均无实根,所以方程
均无实根,所以方程![]() 的实根个数为3,即
的实根个数为3,即![]() ;因
;因![]() 是奇函数,先考虑
是奇函数,先考虑![]() 的图象,因
的图象,因![]() ,由
,由![]() 得
得![]() ,可知
,可知![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,又
上递减,又![]() ,
, ![]() ,由图象关于原点对称得
,由图象关于原点对称得![]() 的示意图如图:
的示意图如图:
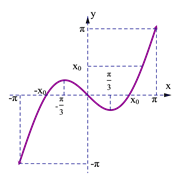
极小值为![]() ,
,
极大值为![]() . 方程
. 方程![]() 的实根为方程
的实根为方程![]()
或![]() 或
或![]() 的根,显然方程
的根,显然方程![]() 有3个根,
有3个根,
方程![]() 与
与![]() 各有1个根,从而方程
各有1个根,从而方程![]()
实根的个数为5,即n=5;记方程![]() 除0外的另外两个实根
除0外的另外两个实根
分别为![]() ,可知
,可知![]() ,方程
,方程![]() 的实根为方程
的实根为方程![]() 或
或![]() 或
或![]() 的根,显然方程
的根,显然方程![]() 有3个根,方程
有3个根,方程![]() 与
与![]() 各有1个根,从而方程
各有1个根,从而方程![]() 根的个数为5,即t=5,故
根的个数为5,即t=5,故![]() 13.故选B.
13.故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15℃,B点表示四月的平均最低气温约为5℃.下面叙述不正确的是 ( )
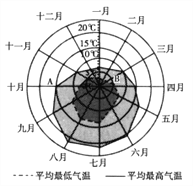
A. 各月的平均最低气温都在0℃以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于20℃的月份有5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图所示,据此解答如下问题:

(1)求高三(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析女生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条直线l1:4x+y-4=0,l2:mx+y=0,l3:2x-3my-4=0.
(1)若直线l1,l2,l3交于一点,求实数m的值;
(2)若直线l1,l2,l3不能围成三角形,求实数m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.下图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知
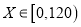 ,历年中日泄流量在区间[30,60)
,历年中日泄流量在区间[30,60)的年平均天数为156,一年按364天计.
(Ⅰ)请把频率分布直方图补充完整;
(Ⅱ)该水电站希望安装的发电机尽可能运行,但每30万立方米的日泄流量才够运行一台发电机,如
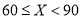 时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机?
时才够运行两台发电机,若运行一台发电机,每天可获利润为4000元,若不运行,则该台发电机每天亏损500元,以各段的频率作为相应段的概率,以水电站日利润的期望值为决策依据,问:为使水电站日利润的期望值最大,该水电站应安装多少台发电机? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=sinx-
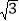 cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+
cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+ ))(0<α<
))(0<α< ),且a·b=
),且a·b= .
.(1)求f(x)在区间
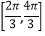 上的最值;
上的最值;(2)求
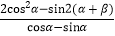 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
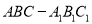 中,
中,  为
为 上的点,
上的点, 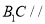 平面
平面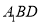 ;
;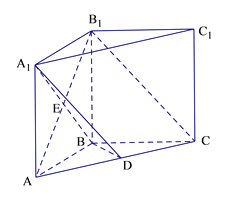
(Ⅰ)求证:
 平面
平面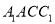 ;
;(Ⅱ)若
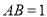 ,且
,且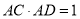 ,求二面角
,求二面角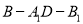 的余弦值.
的余弦值.
相关试题

