【题目】在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.
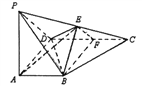
(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() ,若平面
,若平面![]() 与平面
与平面![]() 所成锐二面角
所成锐二面角![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)详见解析; (2)![]() .
.
【解析】试题分析:(1) 求证:平面ABE⊥平面BEF, 只需证明一个平面过另一个平面的垂线即可, 注意到AB∥CD,CD⊥AD,AD = 2AB,而![]() 分别为
分别为![]() 的中点,可得四边形ABCD为矩形,说明AB⊥BF,再证明AB⊥EF,由线面垂直的判定可得AB⊥面BEF,再根据面面垂直的判定得到平面ABE⊥平面BEF;(2)以A点为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立空间坐标系,利用平面法向量所成交与二面角的关系求出二面角的余弦值,根据给出的二面角的范围得其余弦值的范围,最后求解不等式可得a的取值范围.
的中点,可得四边形ABCD为矩形,说明AB⊥BF,再证明AB⊥EF,由线面垂直的判定可得AB⊥面BEF,再根据面面垂直的判定得到平面ABE⊥平面BEF;(2)以A点为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立空间坐标系,利用平面法向量所成交与二面角的关系求出二面角的余弦值,根据给出的二面角的范围得其余弦值的范围,最后求解不等式可得a的取值范围.
试题解析:(Ⅰ)![]()
![]()
![]()
![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]()
![]() 为矩形,
为矩形,![]() 2分
2分
∵DE=EC,∴DC⊥EF,又AB∥CD,∴AB⊥EF
∵BF∩EF=F,∴AB⊥面BEF,又AE面ABE,
∴平面ABE⊥平面BEF. 4分
(Ⅱ)![]() ,又
,又![]() ,
,![]()
又![]() ,所以
,所以![]() 面
面![]() ,
,![]() 6分
6分
法一:建系![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
![]()
![]() ,
,![]() ,
,![]()
平面![]() 法向量
法向量![]() ,平面
,平面![]() 法向量
法向量![]() ·9分
·9分
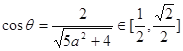 ,可得
,可得![]() . 12分
. 12分
法二:连![]() 交
交![]() 于点
于点![]() ,四边形
,四边形![]() 为平行四边形,所以
为平行四边形,所以![]() 为
为![]() 的中点,连
的中点,连![]() ,
,
则![]() ,
,![]() 面
面![]() ,
,![]() ,
,
作![]() 于
于![]() 点,所以
点,所以![]() 面
面![]() ,
,
连![]() ,则
,则![]() ,
,![]() 即为所求 9分
即为所求 9分
在![]() 中,
中,![]() ,
,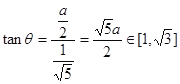
解得![]() 12 分
12 分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,P在对角线BD1上,且BP=
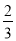 BD1,给出下面四个命题:
BD1,给出下面四个命题:(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三点共线;(4)平面MNQ∥平面APC.正确的序号为 ( )
A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,求函数
时,求函数 在区间
在区间 上的最大值与最小值;
上的最大值与最小值;(2)若在
 上存在
上存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在
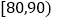 的人数为12人.
的人数为12人.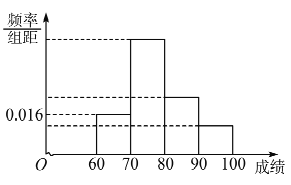
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为
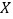 ,求
,求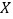 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
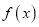 的定义域为
的定义域为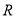 ,对于任意的
,对于任意的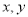 都有
都有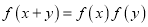 ,设
,设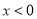 时,
时, 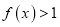 .
.(1)求
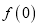 ;
;(2)证明:对于任意的
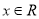 ,
, 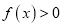 ;
;(3)当
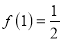 时,若不等式
时,若不等式 在
在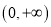 上恒定成立,求实数
上恒定成立,求实数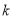 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:
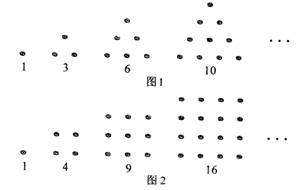
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A. 36 B. 45 C. 99 D. 100
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一段演绎推理:“直线平行于平面,则这条直线平行于平面内所有直线;已知直线
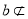 平面
平面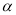 ,直线
,直线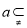 平面
平面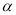 ,直线
,直线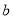 ∥平面
∥平面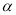 ,则直线
,则直线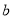 ∥直线
∥直线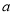 ”的结论是错误的,这是因为 ( )
”的结论是错误的,这是因为 ( )A. 大前提错误 B. 小前提错误 C. 推理形式错误 D. 非以上错误
相关试题

