【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的最大值与最小值;
上的最大值与最小值;
(2)若在![]() 上存在
上存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,
, ![]() ;(2)
;(2)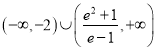 .
.
【解析】试题分析:(1)由![]() 得增区间
得增区间![]() ,
, ![]() 得减区间
得减区间![]() ,进而得
,进而得![]() ,比较端点处函数值可得
,比较端点处函数值可得![]() ;(2)只需要函数
;(2)只需要函数![]() 在
在![]() 上的最小值小于零,利用导数研究
上的最小值小于零,利用导数研究![]() 的单调性,讨论三种情况,分别求得
的单调性,讨论三种情况,分别求得![]() 的最小值,进而分别求得
的最小值,进而分别求得![]() 的取值范围,求并集即可.
的取值范围,求并集即可.
试题解析:(1)当![]() 时,
时, ![]()
![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
| 0 |
|
|
| 极小值 |
|
因为![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 在区间
在区间![]() 上的最大值与最小值分别为:
上的最大值与最小值分别为:
![]() ,
, ![]() .
.
(2)设![]() .若在
.若在![]() 上存在
上存在![]() ,使得
,使得![]() ,即
,即![]() 成立,则只需要函数
成立,则只需要函数![]() 在
在![]() 上的最小值小于零.
上的最小值小于零.
又![]()
![]()
令![]() ,得
,得![]() (舍去)或
(舍去)或![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,
上单调递减,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由
,由![]() ,可得
,可得![]() .
.
因为![]() ,所以
,所以![]() .
.
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
故![]() 在
在![]() 上的最小值为
上的最小值为![]() ,由
,由![]() ,
,
可得![]() (满足
(满足![]() ).
).
③当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
因为![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,不满足题意,舍去.
,不满足题意,舍去.
综上可得![]() 或
或![]() ,
,
所以实数![]() 的取值范围为
的取值范围为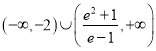 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)是R上的偶函数,对x∈R都有f(x+4)=f(x)+f(2)成立.当x1,x2∈[0,2],且x1≠x2时,都有
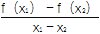 <0,给出下列命题:
<0,给出下列命题:①f(2)=0;
②直线x=-4是函数y=f(x)图象的一条对称轴;
③函数y=f(x)在[-4,4]上有四个零点;
④f(2 014)=0.
其中所有正确命题的序号为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用二分法求
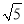 的近似值(精确度0.1).
的近似值(精确度0.1). -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,P在对角线BD1上,且BP=
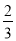 BD1,给出下面四个命题:
BD1,给出下面四个命题:(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三点共线;(4)平面MNQ∥平面APC.正确的序号为 ( )
A. (1)(2) B. (1)(4) C. (2)(3) D. (3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在
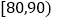 的人数为12人.
的人数为12人.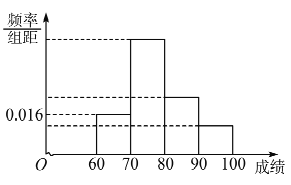
(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为
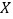 ,求
,求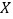 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
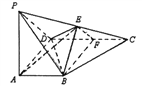
查看答案和解析>>【题目】在四棱锥
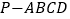 中,
中,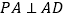 ,
,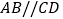 ,
,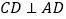 ,
,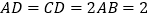 ,
,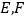 分别为
分别为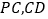 的中点,
的中点,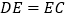 .
.
(1)求证:平面
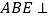 平面
平面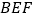 ;
;(2)设
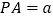 ,若平面
,若平面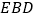 与平面
与平面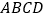 所成锐二面角
所成锐二面角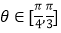 ,求
,求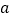 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
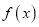 的定义域为
的定义域为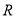 ,对于任意的
,对于任意的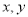 都有
都有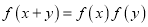 ,设
,设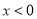 时,
时, 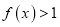 .
.(1)求
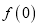 ;
;(2)证明:对于任意的
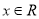 ,
, 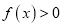 ;
;(3)当
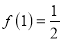 时,若不等式
时,若不等式 在
在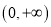 上恒定成立,求实数
上恒定成立,求实数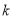 的取值范围.
的取值范围.
相关试题

