【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
参考答案:
【答案】
(1)解:∵a1=1,an+1═ ![]() ,
,
∴ ![]() ,
,
即 ![]() =
= ![]() =3(
=3( ![]() +
+ ![]() ),
),
则{ ![]() +
+ ![]() }为等比数列,公比q=3,
}为等比数列,公比q=3,
首项为 ![]() ,
,
则 ![]() +
+ ![]() =
= ![]() ,
,
即 ![]() =﹣
=﹣ ![]() +
+ ![]() =
= ![]() ,即an=
,即an= ![]()
(2)解:bn=(3n﹣1) ![]() an=
an= ![]() ,
,
则数列{bn}的前n项和Tn= ![]() ①
①
![]() =
= ![]()
![]() +…+
+…+ ![]() ②,
②,
两式相减得 ![]() =1
=1 ![]() ﹣
﹣ ![]() =
= ![]() =2﹣
=2﹣ ![]() ﹣
﹣ ![]() =2﹣
=2﹣ ![]() ,
,
则 Tn=4﹣ ![]()
【解析】(1)根据数列的递推关系,结合等比数列的定义即可证明{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;(2)利用错误相减法即可求出数列的和.
}为等比数列,并求{an}的通项公式an;(2)利用错误相减法即可求出数列的和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 与
与 是
是 的子集,若
的子集,若 ,则称
,则称 为一个“理想配集”,那么符合此条件的“理想配集”的个数是________.(规定
为一个“理想配集”,那么符合此条件的“理想配集”的个数是________.(规定 与
与 是两个不同的“理想配集”)
是两个不同的“理想配集”) -
科目: 来源: 题型:
查看答案和解析>>【题目】用半径为R的圆铁皮剪一个内接矩形,再以内接矩形的两边分别作为圆柱的高与底面半径,则圆柱的体积最大时,该圆铁皮面积与其内接矩形的面积比为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}中an=
 (n∈N*),将数列{an}中的整数项按原来的顺序组成数列{bn},则b2018的值为( )
(n∈N*),将数列{an}中的整数项按原来的顺序组成数列{bn},则b2018的值为( )
A.5035
B.5039
C.5043
D.5047 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 及直线
及直线 ,直线
,直线 被圆
被圆 截得的弦长为
截得的弦长为 .
.(
 )求实数
)求实数 的值.
的值.(
 )求过点
)求过点 并与圆
并与圆 相切的切线方程.
相切的切线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 中,各个侧面均是边长为
中,各个侧面均是边长为 的正方形,
的正方形, 为线段
为线段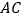 的中点
的中点
(Ⅰ)求证:
 ⊥平面
⊥平面 ;
;(Ⅱ)求证:直线
 ∥平面
∥平面 ;
;(Ⅲ)设
 为线段
为线段 上任意一点,在
上任意一点,在 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点 ,使
,使 ,并说明理由
,并说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, ,
, ,
, ,
, ,
, 、
、 分为
分为 、
、 的中点,
的中点, .
.(
 )求证:平面
)求证:平面 平面
平面 .
.(
 )若
)若 ,求四面体
,求四面体 的体积.
的体积.(
 )设
)设 ,若平面
,若平面 与平面
与平面 所成锐二面角
所成锐二面角 ,求
,求 的取值范围.
的取值范围.
相关试题

