【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为![]() 元, 求
元, 求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)分布列见解析,
;(3)分布列见解析,![]() .
.
【解析】试题分析:(1)直接根据古典概型概率公式求解即可;(2)先求出该会员第一次消费、第二次消费公司获得的利润,然后求平均值即可;(3)![]() 的所有可能取值为
的所有可能取值为![]() 分别求出各随机变量对应的概率,利用期望公式求解即可.
分别求出各随机变量对应的概率,利用期望公式求解即可.
试题解析:(1)![]() 位会员中, 至少消费两次的会员有
位会员中, 至少消费两次的会员有![]() 人, 所以估计一位会员至少消费两次的概率为
人, 所以估计一位会员至少消费两次的概率为![]() .(2)该会员第一次消费时, 公司获得利润为
.(2)该会员第一次消费时, 公司获得利润为![]() (元), 第
(元), 第![]() 次消费时, 公司获得利润为
次消费时, 公司获得利润为![]() (元), 所以, 公司这两次服务的平均利润为
(元), 所以, 公司这两次服务的平均利润为![]() (元).
(元).
(3)由(2)知,一位会员消费次数可能为![]() 次,
次, ![]() 次,
次, ![]() 次,
次, ![]() 次,
次, ![]() 次,当会员仅消费
次,当会员仅消费![]() 次时, 利润为
次时, 利润为![]() 元,当会员仅消费
元,当会员仅消费![]() 次时, 平均利润为
次时, 平均利润为![]() 元,当会员仅消费
元,当会员仅消费![]() 次时, 平均利润为
次时, 平均利润为![]() 元,当会员仅消费
元,当会员仅消费![]() 次时, 平均利润为
次时, 平均利润为![]() 元,当会员仅消费
元,当会员仅消费![]() 次时, 平均利润为
次时, 平均利润为![]() 元,故
元,故![]() 的所有可能取值为
的所有可能取值为![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
![]() 数学期望为
数学期望为![]() (元).
(元).
-
科目: 来源: 题型:
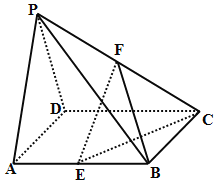
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
(1)求证:EF∥平面PAD;
(2)求三棱锥B-EFC的体积;
(3)求二面角P-EC-D的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家计划在2012年举行商品促销活动,经调查测算,该商品的年销售量
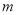 万件与年促销费用
万件与年促销费用 万元满足:
万元满足: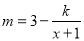 ,其中
,其中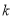 为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).
为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).(1)将2012年该产品的利润
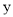 万元表示为年促销费用
万元表示为年促销费用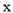 万元的函数;
万元的函数;(2)该厂2012年的促销费用投入多少万元时,厂家的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
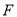 是拋物线
是拋物线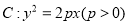 的焦点, 若点
的焦点, 若点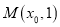 在
在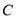 上,且
上,且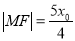 .
.(1)求
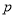 的值;
的值;(2)若直线
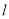 经过点
经过点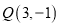 且与
且与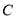 交于
交于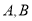 (异于
(异于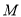 )两点, 证明: 直线
)两点, 证明: 直线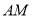 与直线
与直线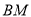 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 四棱锥
 中, 平面
中, 平面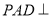 平面
平面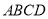 ,
, 为线段
为线段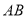 上一点,
上一点, 为
为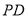 的中点.
的中点.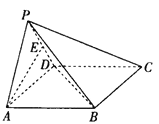
(1)证明:
 平面
平面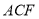 ;
;(2)求二面角
 的正弦值.
的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
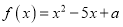 .
.(1)当
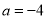 时,求不等式
时,求不等式 的解集;
的解集; (2)对任意
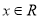 ,若
,若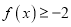 恒成立,求实数
恒成立,求实数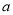 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的极坐标方程是
的极坐标方程是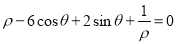 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为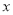 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系 中, 直线
中, 直线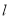 经过点
经过点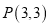 ,倾斜角
,倾斜角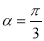 .
.(1)写出曲线
 直角坐标方程和直线
直角坐标方程和直线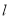 的参数方程;
的参数方程;(2)设
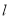 与曲线
与曲线 相交于
相交于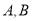 两点, 求
两点, 求 的值.
的值.
相关试题

