【题目】如图, 四棱锥![]() 中, 平面
中, 平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 为
为![]() 的中点.
的中点.
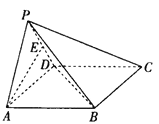
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,设
,设![]() ,可证四边形
,可证四边形![]() 为平行四边形,得
为平行四边形,得![]() 是
是![]() 的中点,利用三角形中位线定理可得
的中点,利用三角形中位线定理可得![]() 进而由线面平行的判定定理可得结论;(2)先证
进而由线面平行的判定定理可得结论;(2)先证![]() 平面
平面![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 为
为![]() 轴正方向,空间直角坐标系
轴正方向,空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,利用空间向量夹角余弦公式可得二面角
的法向量,利用空间向量夹角余弦公式可得二面角![]() 的余弦值,进而得结果.
的余弦值,进而得结果.
试题解析:(1)证明: 连接![]() ,设
,设![]() ,连接
,连接![]() ,
,![]() 四边形
四边形![]() 为平行四边形, 且
为平行四边形, 且![]() 是
是![]() 的中点, 又
的中点, 又![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
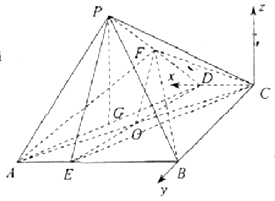
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由
,由![]() 得
得![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() 平面
平面![]() ,在
,在![]() 中,
中,![]() , 在等腰
, 在等腰![]() 中,
中,![]() , 以
, 以![]() 为坐标原点, 分别以
为坐标原点, 分别以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 为
为![]() 轴正方向, 建立如图所示的空间直角坐标系
轴正方向, 建立如图所示的空间直角坐标系![]() ,由题知,
,由题知,![]()
设![]() 是平面
是平面![]() 的法向量, 则
的法向量, 则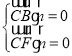 ,即
,即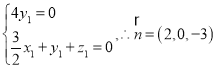 .
.
设![]() 是平面
是平面![]() 的法向量, 则
的法向量, 则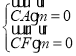 ,即
,即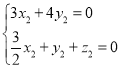 得
得![]() .
.
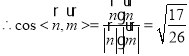 ,
,![]() 二面角
二面角![]() 的正弦值为
的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家计划在2012年举行商品促销活动,经调查测算,该商品的年销售量
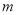 万件与年促销费用
万件与年促销费用 万元满足:
万元满足: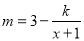 ,其中
,其中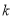 为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).
为常数,若不搞促销活动,则该产品的年销售量只有1万件,已知2012年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家的产量等于销售量,而销售收入为生产成本的1.5倍(生产成本由固定投入和再投入两部分资金组成).(1)将2012年该产品的利润
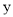 万元表示为年促销费用
万元表示为年促销费用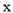 万元的函数;
万元的函数;(2)该厂2012年的促销费用投入多少万元时,厂家的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
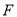 是拋物线
是拋物线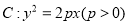 的焦点, 若点
的焦点, 若点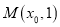 在
在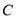 上,且
上,且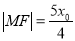 .
.(1)求
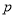 的值;
的值;(2)若直线
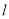 经过点
经过点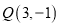 且与
且与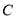 交于
交于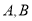 (异于
(异于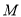 )两点, 证明: 直线
)两点, 证明: 直线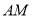 与直线
与直线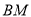 的斜率之积为常数.
的斜率之积为常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按
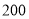 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:消费次第
第
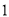 次
次第
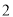 次
次第
 次
次第
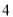 次
次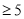 次
次收费比例
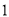
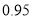
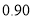
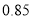
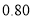
该公司从注册的会员中, 随机抽取了
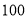 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:消费次第
第
 次
次第
 次
次第
 次
次第
 次
次第
 次
次频数
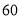
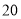
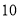

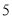
假设汽车美容一次, 公司成本为
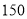 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为
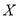 元, 求
元, 求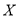 的分布列和数学期望
的分布列和数学期望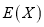 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
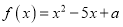 .
.(1)当
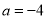 时,求不等式
时,求不等式 的解集;
的解集; (2)对任意
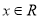 ,若
,若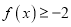 恒成立,求实数
恒成立,求实数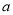 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
 的极坐标方程是
的极坐标方程是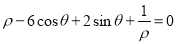 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为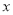 轴的正半轴, 建立平面直角坐标系,在平面直角坐标系
轴的正半轴, 建立平面直角坐标系,在平面直角坐标系 中, 直线
中, 直线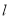 经过点
经过点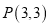 ,倾斜角
,倾斜角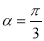 .
.(1)写出曲线
 直角坐标方程和直线
直角坐标方程和直线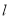 的参数方程;
的参数方程;(2)设
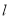 与曲线
与曲线 相交于
相交于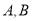 两点, 求
两点, 求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数
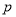 与听课时间
与听课时间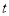 (单位:分钟)之间的关系满足如图所示的曲线.当
(单位:分钟)之间的关系满足如图所示的曲线.当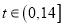 时,曲线是二次函数图象的一部分,当
时,曲线是二次函数图象的一部分,当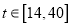 时,曲线是函数
时,曲线是函数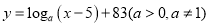 图象的一部分.根据专家研究,当注意力指数
图象的一部分.根据专家研究,当注意力指数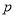 大于80时学习效果最佳.
大于80时学习效果最佳.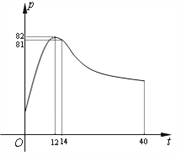
(1)试求
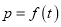 的函数关系式;
的函数关系式;(2)教师在什么时段内安排核心内容,能使得学生学习效果最佳?请说明理由.
相关试题

