【题目】如图所示,某小区准备将闲置的一直角三角形(其中∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.
a)地块开发成公共绿地,设计时,要求绿地部分有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′落在边BC上,设∠AMN=θ.

(1)若θ=![]() 时,绿地“最美”,求最美绿地的面积;
时,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民的行走,设计时要求将AN,A′N的值设计最短,求此时绿地公共走道的长度.
参考答案:
【答案】见解析
【解析】解 (1)由∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() .
.
设MA=MA′=xa(0<x<1),则MB=a-xa,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() .
.
由于△AMN为等边三角形,
所以绿地的面积
S=2×![]() ×
×![]() a×
a×![]() a×sin
a×sin![]() =
=![]() a2.
a2.
(2)因为在Rt△ABC中,∠B=![]() ,AB=a,BC=
,AB=a,BC=![]() a,
a,
所以∠BAC=![]() ,所以在△AMN中,∠ANM=
,所以在△AMN中,∠ANM=![]() -θ,
-θ,
由正弦定理得![]() =
= ,
,
设AM=ax(0<x<1),则A′M=ax,BM=a-ax,
所以在Rt△MBA′中,cos(π-2θ)=![]() =
=![]() ,
,
所以x=![]() ,即AM=
,即AM=![]() ,
,
所以AN=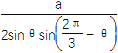 .
.
2sinθsin![]() =sin2θ+
=sin2θ+![]() sinθcosθ
sinθcosθ
=![]() +
+![]() sin2θ-
sin2θ-![]() cos2θ=
cos2θ=![]() +sin(2θ-
+sin(2θ-![]() ),
),
因为![]() <θ<
<θ<![]() ,所以
,所以![]() <2θ-
<2θ-![]() <
<![]() ,
,
所以当且仅当2θ-![]() =
=![]() ,即θ=
,即θ=![]() 时,AN的值最小,且AN=
时,AN的值最小,且AN=![]() a,此时绿地公共走道的长度MN=
a,此时绿地公共走道的长度MN=![]() a.
a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
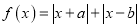 .
.(1)当
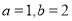 时,求不等式
时,求不等式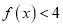 的解集;
的解集;(2)若
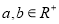 ,且
,且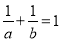 ,求证:
,求证: 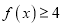 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
-
科目: 来源: 题型:
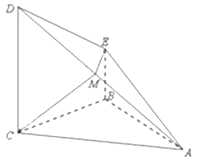
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 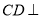 平面
平面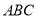 ,
, 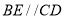 ,
, 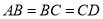 ,
, 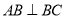 ,
, 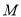 为
为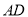 上一点,
上一点, 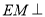 平面
平面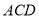 .
.
(Ⅰ)证明:
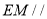 平面
平面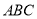 ;
;(Ⅱ)若
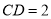 ,求四棱锥
,求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量m=(cosx,-1),n=
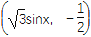 ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.(1)求函数f(x)的最小正周期;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=1,c=
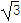 ,且f(A)恰是函数f(x)在
,且f(A)恰是函数f(x)在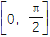 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照
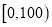 ,
, 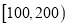 ,
, 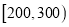 ,
, 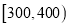 ,
, 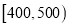 ,
, 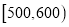 ,
, 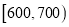 ,
, 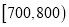 ,
, 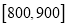 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.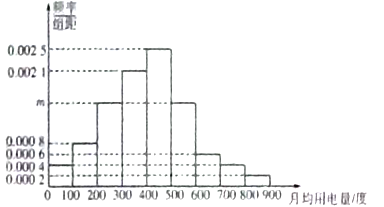
(Ⅰ)求直方图中
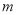 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
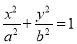 (a>b>0)的离心率为
(a>b>0)的离心率为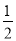 ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+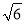 =0相切.
=0相切.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣
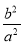 ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
相关试题

