搜索
【题目】已知椭圆C： 
（a＞b＞0）的离心率为
，以原点O为圆心，椭圆的短半轴长为半径的圆与直线x﹣y+
=0相切．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l：y=kx+m与椭圆C相交于A、B两点，且kOAkOB=﹣
，判断△AOB的面积是否为定值？若为定值，求出定值；若不为定值，说明理由．
参考答案：
【答案】（1）
（2）
【解析】试题分析：（1）由椭圆的离心率等于
，原点
到直线
的距离等于
及隐含条件
联立方程组求解
的值，则椭圆
的标准方程可求；（2）联立直线方程和椭圆方程，消去
后利用根与系数关系得到
两点的横坐标的和与积，由弦长公式求得
，由点到直线的距离公式求得
到
的距离，代入三角形的面积公式证得答案.
试题解析：（1）由题意得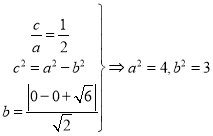
椭圆的方程为
.
（2）设
， 
则A,B的坐标满足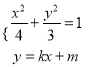
消去y化简得
， 
，
得
， 
=
，即
即
=
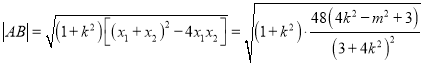
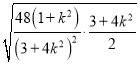
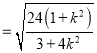
O到直线
的距离
=
=
=
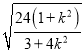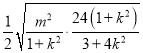为定值
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某小区准备将闲置的一直角三角形(其中∠B＝
，AB＝a，BC＝
a)地块开发成公共绿地，设计时，要求绿地部分有公共绿地走道MN，且两边是两个关于走道MN对称的三角形(△AMN和△A′MN)，现考虑方便和绿地最大化原则，要求M点与B点不重合，A′落在边BC上，设∠AMN＝θ.
(1)若θ＝
时，绿地“最美”，求最美绿地的面积；(2)为方便小区居民的行走，设计时要求将AN，A′N的值设计最短，求此时绿地公共走道的长度.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量m＝(cosx，－1)，n＝
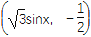，函数f(x)＝(m＋n)·m.(1)求函数f(x)的最小正周期；
(2)已知a，b，c分别为△ABC内角A，B，C的对边，A为锐角，a＝1，c＝
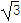，且f(A)恰是函数f(x)在
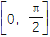上的最大值，求A，b和△ABC的面积. -
科目： 来源： 题型：
查看答案和解析>>【题目】某市为了制定合理的节电方案，供电局对居民用电进行了调查，通过抽样，获得了某年200户居民每户的月均用电量（单位：度），将数据按照
， 
， 
， 
， 
， 
， 
， 
， 
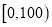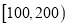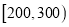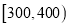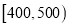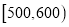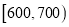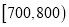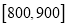分成9组，制成了如图所示的频率分布直方图．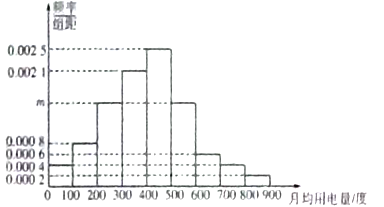
（Ⅰ）求直方图中
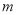的值并估计居民月均用电量的中位数；（Ⅱ）现从第8组和第9组的居民中任选取2户居民进行访问，则两组中各有一户被选中的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2，3，4，乙袋中红色、黑色、白色小球的个数均为3，某人用左右手分别从甲、乙两袋中取球．
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若左右手依次各取两球，称同一手中两球颜色相同的取法为成功取法，记两次取球（左右手依次各取两球为两次取球）的成功取法次数为随机变量X，求X的分布列。
-
科目： 来源： 题型：
查看答案和解析>>【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况，在一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度x（单位：辆/千米）的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数．
（Ⅰ）当0≤x≤200时，求函数v（x）的表达式；
（Ⅱ）当车流密度x为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时）f（x）=xv（x）可以达到最大，并求出最大值．（精确到1辆/小时）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆
： 
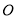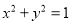过椭圆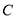
： 
(
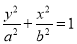)的短轴端点，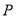 
， 
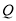分别是圆
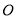与椭圆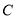
上任意两点，且线段
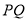长度的最大值为3．（Ⅰ）求椭圆
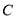的方程；（Ⅱ）过点
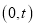作圆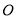
的一条切线交椭圆
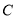于
， 
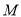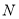两点，求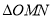
的面积的最大值．
相关试题
