【题目】数列![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]()
(Ⅰ)判断![]() 与
与![]() 的大小关系,并证明你的结论;
的大小关系,并证明你的结论;
(Ⅱ)求证: ![]() .
.
参考答案:
【答案】(1)当n为奇数时, ![]() ,即
,即![]() <
<![]() ;当n为偶数时,
;当n为偶数时, ![]() ,
, ![]() >
>![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(Ⅰ) 分当![]() 为奇数时和当n为偶数时两种情况,将
为奇数时和当n为偶数时两种情况,将![]() 与2作差,变形即可判断
与2作差,变形即可判断![]() 与
与![]() 的大小关系;
的大小关系;
(Ⅱ) 要证![]() ,
,
只需证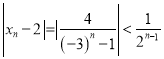 ,验证可知当
,验证可知当![]() 时,当
时,当![]() 时不等式成立,
时不等式成立,
当![]() 为偶数且
为偶数且![]() 时,
时,
要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,
,
令![]() ,则
,则![]() 单调递减,即可证明;
单调递减,即可证明;
当![]() 为奇数且
为奇数且![]() 时,要证
时,要证![]() ,只需证
,只需证![]() ,
,
只需证![]() ,即证
,即证![]() ,令
,令![]() ,讨论单调性即可证明.
,讨论单调性即可证明.
试题解析:Ⅰ) 当n为奇数时, ![]() <
<![]() ;当n为偶数时,
;当n为偶数时, ![]() >
>![]() . 证明如下:
. 证明如下:
![]() ,
,
两边同取倒数得:
![]() ,
,
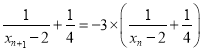 ,
,
所以数列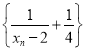 是以
是以![]() 为首项,
为首项, ![]() 为公比的等比数列,
为公比的等比数列, ![]() ,
, ![]() ,所以当n为奇数时,
,所以当n为奇数时,
![]() ,即
,即![]() <
<![]() ;当n为偶数时,
;当n为偶数时, ![]() ,
, ![]() >
>![]() .
.
(Ⅱ)证明:因为
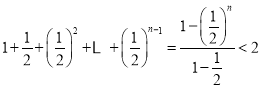 ,
,
要证![]() ,
,
只需证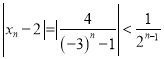 ,
,
当![]() 时,
时, ![]() 成立,当
成立,当![]() 时,
时, ![]() 成立,
成立,
当![]() 为偶数且
为偶数且![]() 时,
时,
要证![]() ,
,
只需证![]() ,即证
,即证
![]() ,
,
令![]() ,则
,则![]() 单调递减,
单调递减, ![]() ,
,
当![]() 为奇数且
为奇数且![]() 时,
时,
要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
即证![]() ,令
,令![]() ,
,
则![]() 单调递减,
单调递减, ![]() ,
,
所以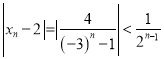 成立,
成立,
所以![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方体
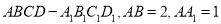 ,直线
,直线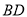 与平面
与平面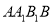 所成角为
所成角为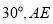 垂直
垂直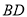 于点
于点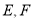 为
为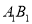 的中点.
的中点.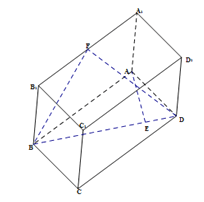
(1)求直线
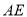 与平面
与平面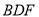 所成角的正弦值;
所成角的正弦值;(2)线段
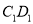 上是否存在点
上是否存在点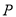 ,使得二面角
,使得二面角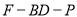 的余弦值为
的余弦值为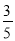 ?若存在,确定
?若存在,确定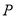 点位置;若不存在,说明理由.
点位置;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018江苏南京师大附中、天一、海门、淮阴四校高三联考】如图,一只蚂蚁从单位正方体
 的顶点
的顶点 出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过
出发,每一步(均为等可能性的)经过一条边到达另一顶点,设该蚂蚁经过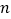 步回到点
步回到点 的概率
的概率 .
.
(I)分别写出
 的值;
的值;(II)设顶点
 出发经过
出发经过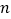 步到达点
步到达点 的概率为
的概率为 ,求
,求 的值;
的值;(III)求
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数按下表排列:

(1)求200在表中的位置(在第几行第几列);
(2)求表中主对角线上的数列:1、3、7、13、21、…的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家电公司根据销售区域将销售员分成
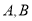 两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间
两组.2017年年初,公司根据销售员的销售业绩分发年终奖,销售员的销售额(单位:十万元)在区间 内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间
内对应的年终奖分别为2万元,2.5万元,3万元,3.5万元.已知200名销售员的年销售额都在区间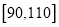 内,将这些数据分成4组:
内,将这些数据分成4组: 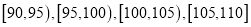 ,得到如下两个频率分布直方图:
,得到如下两个频率分布直方图:
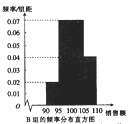
以上面数据的频率作为概率,分别从
 组与
组与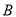 组的销售员中随机选取1位,记
组的销售员中随机选取1位,记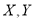 分别表示
分别表示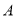 组与
组与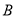 组被选取的销售员获得的年终奖.
组被选取的销售员获得的年终奖.(1)求
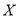 的分布列及数学期;
的分布列及数学期;(2)试问
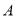 组与
组与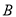 组哪个组销售员获得的年终奖的平均值更高?为什么?
组哪个组销售员获得的年终奖的平均值更高?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】某海产品经销商调查发现,该海产品每售出
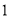 吨可获利
吨可获利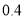 万元,每积压
万元,每积压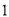 吨则亏损
吨则亏损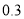 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.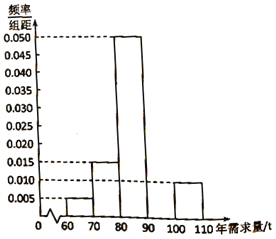
(1)请补齐
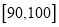 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;(2)今年该经销商欲进货
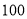 吨,以
吨,以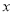 (单位:吨,
(单位:吨, 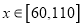 )表示今年的年需求量,以
)表示今年的年需求量,以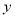 (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将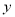 表示为
表示为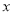 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于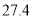 万元的概率.
万元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
:  的焦点为
的焦点为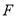 ,圆
,圆 :
:  ,过
,过 作垂直于
作垂直于 轴的直线交抛物线
轴的直线交抛物线 于
于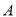 、
、 两点,且
两点,且 的面积为
的面积为 .
.(1)求抛物线
 的方程和圆
的方程和圆 的方程;
的方程;(2)若直线
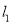 、
、 均过坐标原点
均过坐标原点 ,且互相垂直,
,且互相垂直,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,
,  交抛物线
交抛物线 于
于 ,交圆
,交圆 于
于 ,求
,求 与
与 的面积比的最小值.
的面积比的最小值.
相关试题

