【题目】已知动圆过点![]() ,且被
,且被![]() 轴截得的线段长为4,记动圆圆心的轨迹为曲线
轴截得的线段长为4,记动圆圆心的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)问: ![]() 轴上是否存在一定点
轴上是否存在一定点![]() ,使得对于曲线
,使得对于曲线![]() 上的任意两点
上的任意两点![]() 和
和![]() ,当
,当![]() 时,恒有
时,恒有![]() 与
与![]() 的面积之比等于
的面积之比等于![]() ?若存在,则求
?若存在,则求![]() 点的坐标,否则说明理由.
点的坐标,否则说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,定点
;(2)存在,定点![]() .
.
【解析】试题分析:(1)设动圆圆心的坐标为![]() ,由题意可得
,由题意可得![]()
![]()
![]() ;(2)由
;(2)由![]()
![]() 三点共线
三点共线![]()
![]() 的方程:
的方程: ![]()
![]()
![]()
![]()
![]()
![]() ,由
,由![]() 与
与![]() 的面积之比等于
的面积之比等于![]()
![]()
![]() 平分
平分![]()
![]() 此直线
此直线![]() 的倾斜角互补
的倾斜角互补![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 存在定点
存在定点![]() ,满足条件.
,满足条件.
试题解析:(1)设动圆圆心的坐标为![]() ,由题意可得:
,由题意可得: ![]() ,化为:
,化为: ![]() ,
,
∴动圆圆心的轨迹方程为: ![]() ......................4分
......................4分
(2)设![]() 由
由![]() ,可知:
,可知: ![]() 三点共线,设直线
三点共线,设直线![]() 的方程为:
的方程为: ![]() ,代入抛物线方程可得:
,代入抛物线方程可得: ![]() ,
,
∴![]() ,由
,由![]() 与
与![]() 的面积之比等于
的面积之比等于![]() ,可得:
,可得: ![]() 平分
平分![]() ,
,
因此直线![]() 的倾斜角互补,
的倾斜角互补,
∴![]() ,∴
,∴![]() ,
,
把![]() 代入可得:
代入可得: ![]() ,
,
∴![]() ,化为:
,化为: ![]() ,由于对于任意
,由于对于任意![]() 都 成立,∴
都 成立,∴![]() ,
,
故存在定点![]() ,满足条件...............................12分
,满足条件...............................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为
 ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为 ,而当年产销量相等。
,而当年产销量相等。(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
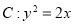 的焦点为
的焦点为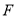 ,平行于
,平行于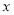 轴的两条直线
轴的两条直线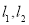 分别交
分别交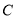 于
于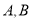 两点,交
两点,交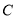 的准线于
的准线于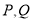 两点 .
两点 .(1)若
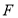 在线段
在线段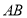 上,
上,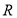 是
是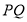 的中点,证明
的中点,证明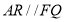 ;
;(2)若
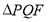 的面积是
的面积是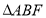 的面积的两倍,求
的面积的两倍,求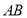 中点的轨迹方程.
中点的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形
 中,
中,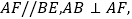 且
且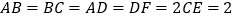 ,沿
,沿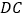 将梯形
将梯形 折起,使得平面
折起,使得平面 ⊥平面
⊥平面
 .
.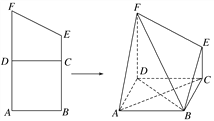
(1)证明:
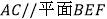 ;
;(2)求三棱锥
 的体积;
的体积;(3)求直线
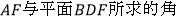 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在三棱柱
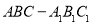 中,已知
中,已知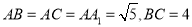 ,点
,点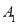 在底面
在底面 的投影是线段
的投影是线段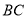 的中点
的中点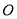 .
.
(1)证明:在侧棱
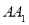 上存在一点
上存在一点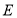 ,使得
,使得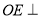 平面
平面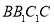 ,并求出
,并求出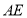 的长;
的长;(2)求:平面
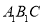 与平面
与平面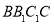 夹角的余弦值.
夹角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】先后2次抛掷一枚骰子,将得到的点数分别记为
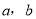 .
.(Ⅰ)求满足
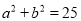 的概率;
的概率;(Ⅱ)设三条线段的长分别为
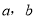 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费
 (单位:千元)对年销售量
(单位:千元)对年销售量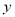 (单位:
(单位:  )和年利润
)和年利润 (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费 和年销售量
和年销售量 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.
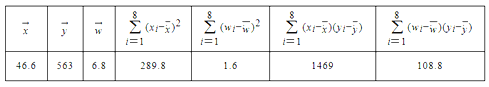
表中
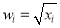 ,
,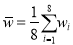 .
.(1)根据散点图判断,
 与
与 哪一个适宜作为年销售量
哪一个适宜作为年销售量 关于年宣传费
关于年宣传费 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立
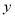 关于
关于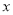 的回归方程;
的回归方程;(3)已知这种产品的年利润
 与
与 、
、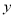 的关系为
的关系为 .根据(2)的结果要求:年宣传费
.根据(2)的结果要求:年宣传费 为何值时,年利润最大?
为何值时,年利润最大?附:对于一组数据
 ,
,  ,…,
,…,  其回归直线
其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为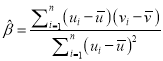 ,
,  .
.
相关试题

