【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)消去参数![]() 得到
得到![]() 的普通方程为
的普通方程为![]() .利用
.利用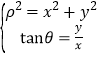 可以把
可以把![]() 的极坐标方程化为直角坐标方程.
的极坐标方程化为直角坐标方程.
(2)把![]() 的直角方程转化为参数方程,利用点到直线的距离公式算出距离为
的直角方程转化为参数方程,利用点到直线的距离公式算出距离为![]() ,利用
,利用![]() 得到
得到![]() .因为直线与椭圆是相离的,所以
.因为直线与椭圆是相离的,所以![]() 或
或![]() ,分类讨论就可以得到
,分类讨论就可以得到![]() 相应的值.
相应的值.
解析:(1)由曲线![]() 的参数方程,消去参数
的参数方程,消去参数![]()
![]() ,可得
,可得![]()
![]() 的普通方程为:
的普通方程为:![]() .
.
由曲线![]() 的极坐标方程得
的极坐标方程得![]() , ∴曲线
, ∴曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)设曲线![]() 上任意一点
上任意一点![]() 为
为![]() ,
,![]() ,则点
,则点![]() 到曲线
到曲线![]()
![]() 的距离为
的距离为![]() .∵
.∵![]() , ∴
, ∴![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .∴
.∴![]() 或
或![]() .
.
-
科目: 来源: 题型:
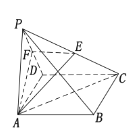
查看答案和解析>>【题目】如图,在四棱锥
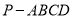 中,
中, 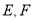 分别是
分别是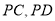 的中点,底面
的中点,底面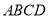 是边长为2的正方形,
是边长为2的正方形, 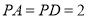 ,且平面
,且平面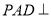 平面
平面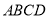 .
.
(1)求证:平面
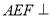 平面
平面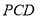 ;
;(2)求平面
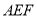 与平面
与平面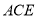 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知短轴长为2的椭圆
 ,直线
,直线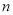 的横、纵截距分别为
的横、纵截距分别为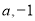 ,且原点到直线
,且原点到直线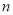 的距离为
的距离为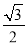 .
.(1)求椭圆
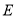 的方程;
的方程;(2)直线
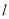 经过椭圆的右焦点
经过椭圆的右焦点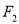 且与椭圆
且与椭圆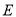 交于
交于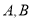 两点,若椭圆
两点,若椭圆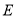 上存在一点
上存在一点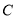 满足
满足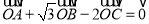 ,求直线
,求直线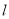 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
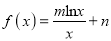 ,
, 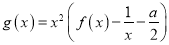 (
(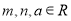 ),且曲线
),且曲线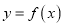 在点
在点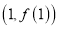 处的切线方程为
处的切线方程为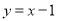 .
.(1)求实数
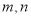 的值及函数
的值及函数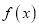 的最大值;
的最大值;(2)当
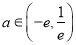 时,记函数
时,记函数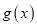 的最小值为
的最小值为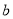 ,求
,求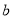 的取值范围.
的取值范围. -
科目: 来源: 题型:
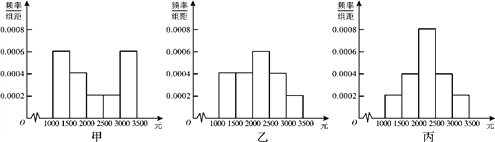
查看答案和解析>>【题目】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系为__________.(用“>”连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
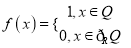 ,则(ⅰ)
,则(ⅰ)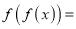 ____________.
____________.(ⅱ)给出下列三个命题:①函数
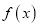 是偶函数;②存在
是偶函数;②存在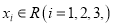 ,使得以点
,使得以点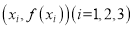 为顶点的三角形是等腰三角形;③存在
为顶点的三角形是等腰三角形;③存在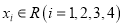 ,使得以点
,使得以点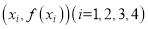 为顶点的四边形为菱形.
为顶点的四边形为菱形.其中,所有真命题的序号是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为
 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:(Ⅰ)写出
 ,
,  ,
,  ,
,  的值.
的值.(Ⅱ)在选取的样本中,从竞赛成绩是
 分以上(含
分以上(含 分)的同学中随机抽取
分)的同学中随机抽取 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的 名同学来自同一组的概率.
名同学来自同一组的概率.(Ⅲ)在(Ⅱ)的条件下,设
 表示所抽取的
表示所抽取的 名同学中来自第
名同学中来自第 组的人数,求
组的人数,求 的分布列及其数学期望.
的分布列及其数学期望.组别
分组
频数
频率
第
 组
组


第
 组
组


第
 组
组


第
 组
组


第
 组
组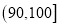


合计



相关试题

