【题目】已知函数![]() (a<0).
(a<0).
(Ⅰ)当a=-3时,求f(x)的单调递减区间;
(Ⅱ)若函数f(x)有且仅有一个零点,求实数a的取值范围;
参考答案:
【答案】(1) 单调递减区间为(-3,-2)和(0,+∞);(2) a<0.
【解析】试题分析:(1)解关于导函数的不等式,得到所求的单调减区间;(2)函数f(x)有且仅有一个零点,即函数图象与x轴有唯一的公共点,利用导函数研究函数图象走势即可.
试题解析:
(Ⅰ)∵a=-3,∴![]() ,故
,故![]()
令f′(x)<0,解得-3<x<-2或x>0,
即所求的单调递减区间为(-3,-2)和(0,+∞)
(Ⅱ)∵![]() (x>a)
(x>a)
令f′(x)=0,得x=0或x=a+1
(1)当a+1>0,即-1<a<0时,f(x)在(a,0)和(a+1,+∞)上为减函数,在(0,a+1)上为增函数.
由于f(0)=aln(-a)>0,当x→a时,f(x)→+∞.
当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,
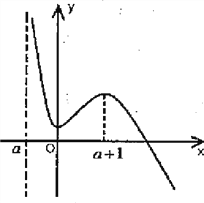
此时函数f(x)有且仅有一个零点.
即当-1<a<0对,f(x)有且仅有一个零点;
(2)当a=-1时,![]() ,
,
∵![]() ,∴f(x)在(a,+∞)单调递减,
,∴f(x)在(a,+∞)单调递减,
又当x→-1时,f(x)→+∞.当x→+∞时,f(x)→-∞,
故函数f(x)有且仅有一个零点;
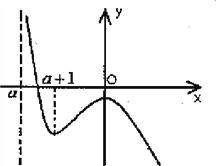
(3)当a+1<0即a<-1时,f(x)在(a,a+1)和(0,+∞)上为减函数,在(a+1,0)上为增函数.又f(0)=aln(-a)<0,当x→a时,f(x)→+∞,当x→+∞时,f(x)→-∞,于是可得函数f(x)图像的草图如图,此时函数f(x)有且仅有一个零点;
综上所述,所求的范围是a<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P—ABCD的底面ABCD为矩形,PA⊥平面ABCD,点E是棱PD的中点,点F是PC的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)若底面ABCD为正方形,
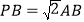 ,求二面角C—AF—D大小.
,求二面角C—AF—D大小.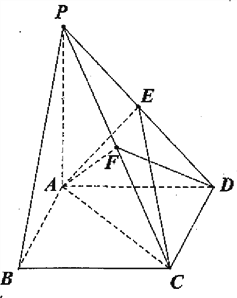
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断下列集合间的关系:
(1)A={x|x-3>2},B={x|2x-5≥0};
(2)A={x∈Z|-1≤x<3},B={x|x=|y|,y∈A}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体
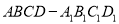 中,
中, 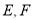 分别为
分别为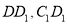 的中点.
的中点.(1)证明:平面
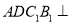 平面
平面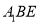 ;
;(2)证明:
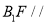 平面
平面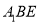 ;
;(3)若正方体棱长为1,求四面体
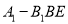 的体积.
的体积.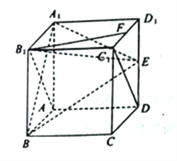
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn,S1=-
 ,an-4SnSn-1=0(n≥2).
,an-4SnSn-1=0(n≥2).(1) 若bn=
 ,求证:{bn}是等差数列;
,求证:{bn}是等差数列;(2) 求数列{an}的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合M={x|x=m+
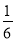 ,m∈Z},N={x|x=
,m∈Z},N={x|x=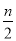 -
-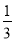 ,n∈Z},P={x|x=
,n∈Z},P={x|x=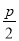 +
+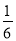 ,p∈Z},试确定M,N,P之间的关系.
,p∈Z},试确定M,N,P之间的关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】在各项都不相等的等差数列{an}中,a1,a2是关于x的方程x2-7a4x+18a3=0的两个实根.
(1) 试判断-22是否在数列{an}中;
(2) 求数列{an}的前n项和Sn的最大值.
相关试题

