【题目】在四棱锥![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为![]() ,求
,求![]() 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】分析:(Ⅰ)连接AC交BE于O,并连接EC,FO,由题意可证得四边形ABCE为平行四边形,则![]() ,
,![]() //平面
//平面![]() .
.
(Ⅱ)由题意可得![]() ,且
,且![]() ,则
,则![]() ,故
,故![]() .
.
(Ⅲ)取![]() 中点
中点![]() ,连
,连![]() ,由题意可知
,由题意可知![]() 的平面角,由几何关系计算可得二面角
的平面角,由几何关系计算可得二面角![]() 的余弦值为
的余弦值为![]() .
.
详解:(Ⅰ)证明:连接AC交BE于O,并连接EC,FO,
![]() ,
,![]() 为
为![]() 中点
中点
![]() AE//BC,且AE=BC
AE//BC,且AE=BC
![]() 四边形ABCE为平行四边形
四边形ABCE为平行四边形
![]() O为AC中点
O为AC中点
又F为AD中点
![]() ,
,
![]() ,
,
![]() //平面
//平面![]()
(Ⅱ)由BCDE为正方形可得![]()
由ABCE为平行四边形可得![]() //
//![]()
![]() 为
为![]() 即
即![]()
![]() ,
,
![]() 侧面
侧面![]() 底面
底面![]() 侧面
侧面![]() 底面
底面![]() 平面
平面![]()
![]() ,
,
![]() ,
,
![]() .
.
(Ⅲ)取![]() 中点
中点![]() ,连
,连![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,
![]() 的平面角,
的平面角,
又![]() ,
,
![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: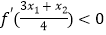 ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记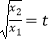 ,求(t﹣1)(a+
,求(t﹣1)(a+ 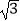 )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为
 ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为  ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x+a|+|x+
 |(a>0)(a<0)
|(a>0)(a<0)
(1)当a=2时,求不等式f(x)>3的解集
(2)证明: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 ,已知
,已知 ,其中
,其中 为原点,
为原点, 为椭圆的离心率.
为椭圆的离心率.(1)求椭圆的方程;
(2)设过点
 的直线
的直线 与椭圆交于点
与椭圆交于点 (
( 不在
不在 轴上),垂直于
轴上),垂直于 的直线与
的直线与 交于点
交于点 ,与
,与 轴交于点
轴交于点 ,若
,若 ,且
,且 ,求直线的
,求直线的 斜率的取值范围.
斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程):
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知射线θ= 与曲线
与曲线  (t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
(t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,直线C的参数方程为
 为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
为参数),曲线P在以该直角坐标系的原点O的为极点,x轴的正半轴为极轴的极坐标系下的方程为ρ2﹣4ρcosθ+3=0.
(1)求直线C的普通方程和曲线P的直角坐标方程;
(2)设直线C和曲线P的交点为A、B,求|AB|.
相关试题

