【题目】已知函数f(x)=|x+a|+|x+ ![]() |(a>0)(a<0)
|(a>0)(a<0)
(1)当a=2时,求不等式f(x)>3的解集
(2)证明: ![]() .
.
参考答案:
【答案】
(1)解:当a=2时,f(x)=|x+2|+|x+ ![]() |,原不等式等价于
|,原不等式等价于 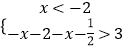
或 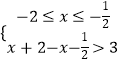 或
或 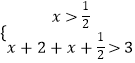
解得:x<﹣ ![]() 或x∈或
或x∈或 ![]() ,所以不等式的解集为{x|x<﹣
,所以不等式的解集为{x|x<﹣ ![]() 或
或 ![]()
(2)解:f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |
|
= ![]()
【解析】(1)分类讨论,解不等式,即可得出结论;(2)f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |,利用三角不等式,及基本不等式即可证明结论.
|,利用三角不等式,及基本不等式即可证明结论.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号,以及对不等式的证明的理解,了解不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
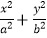 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 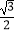 ,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2
,F1、F2分别是椭圆的左、右焦点,M为椭圆上除长轴端点外的任意一点,且△MF1F2的周长为4+2 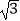 .
.
(1)求椭圆C的方程;
(2)过点D(0,﹣2)作直线l与椭圆C交于A、B两点,点N满足 (O为原点),求四边形OANB面积的最大值,并求此时直线l的方程.
(O为原点),求四边形OANB面积的最大值,并求此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex+ax,(a∈R),其图象与x轴交于A(x1 , 0),B(x2 , 0)两点,且x1<x2
(1)求a的取值范围;
(2)证明: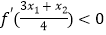 ;(f′(x)为f(x)的导函数)
;(f′(x)为f(x)的导函数)
(3)设点C在函数f(x)的图象上,且△ABC为等边三角形,记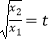 ,求(t﹣1)(a+
,求(t﹣1)(a+ 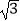 )的值.
)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,已知点P的直角坐标为(1,2),点M的极坐标为
 ,若直线l过点P,且倾斜角为
,若直线l过点P,且倾斜角为  ,圆C以M为圆心,3为半径.
,圆C以M为圆心,3为半径.
(Ⅰ)求直线l的参数方程和圆C的极坐标方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA||PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,侧面
中,侧面 ⊥底面
⊥底面 ,底面
,底面 为直角梯形,
为直角梯形, //
// ,
, ,
, ,
, ,
, 为
为 的中点.
的中点.
(Ⅰ)求证:PA//平面BEF;
(Ⅱ)若PC与AB所成角为
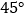 ,求
,求 的长;
的长;(Ⅲ)在(Ⅱ)的条件下,求二面角F-BE-A的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为 ,已知
,已知 ,其中
,其中 为原点,
为原点, 为椭圆的离心率.
为椭圆的离心率.(1)求椭圆的方程;
(2)设过点
 的直线
的直线 与椭圆交于点
与椭圆交于点 (
( 不在
不在 轴上),垂直于
轴上),垂直于 的直线与
的直线与 交于点
交于点 ,与
,与 轴交于点
轴交于点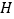 ,若
,若 ,且
,且 ,求直线的
,求直线的 斜率的取值范围.
斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4﹣4:坐标系与参数方程):
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,已知射线θ= 与曲线
与曲线  (t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
(t为参数)相交于A,B来两点,则线段AB的中点的直角坐标为 .
相关试题

