【题目】已知向量 ![]() ,向量
,向量 ![]() ,函数f(x)=
,函数f(x)= ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)将函数y=f(x)的图象上所有点向右平行移动 ![]() 个单位长度,得函数y=g(x)的图象,求函数y=g(x)在区间[0,π]上的值域.
个单位长度,得函数y=g(x)的图象,求函数y=g(x)在区间[0,π]上的值域.
参考答案:
【答案】
(1)解:∵向量 ![]() ,向量
,向量 ![]() ,
,
∴函数f(x)= ![]() =
= ![]() sinx﹣cosx=2sin(x﹣
sinx﹣cosx=2sin(x﹣ ![]() ),
),
令2kπ﹣ ![]() ≤x﹣
≤x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得2kπ﹣
,求得2kπ﹣ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() ,
,
可得函数的增区间为[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z
],k∈Z
(2)解:将函数y=f(x)的图象上所有点向右平行移动 ![]() 个单位长度,
个单位长度,
得函数y=g(x)=2sin(x﹣ ![]() ﹣
﹣ ![]() )=2sin(x﹣
)=2sin(x﹣ ![]() ) 的图象,
) 的图象,
∵x∈[0,π],∴x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],∴g(x)∈[
,1],∴g(x)∈[ ![]() ,2],
,2],
即函数y=g(x)在区间[0,π]上的值域为[ ![]() ,2]
,2]
【解析】(1)利用两个向量的数量积的运算法则求得f(x)的解析式,再利用正弦函数的单调性,求得函数f(x)的单调递增区间.(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的定义域和值域,求得函数y=g(x)在区间[0,π]上的值域.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
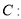
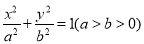 ,
, 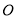 是坐标原点,
是坐标原点,  分别为其左右焦点,
分别为其左右焦点, 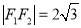 ,
, 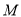 是椭圆上一点,
是椭圆上一点, 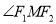 的最大值为
的最大值为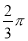
(Ⅰ)求椭圆
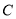 的方程;
的方程;(Ⅱ)若直线
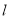 与椭圆
与椭圆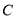 交于
交于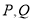 两点,且
两点,且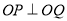
(i)求证:
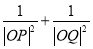 为定值;
为定值;(ii)求
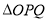 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨<
 )的部分图象如图所示,则f(x)的解析式为( )
)的部分图象如图所示,则f(x)的解析式为( ) 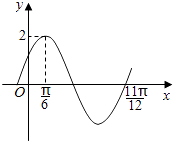
A.f(x)=2sin(x+ )
)
B.f(x)=2sin(2x+ )
)
C.f(x)=2sin(2x﹣ )
)
D.f(x)=2sin(4x﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=
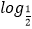 (1﹣x).
(1﹣x).
(1)求f(0),f(1);
(2)求函数f(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 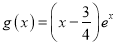 .
.(Ⅰ)若
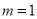 ,求
,求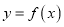 在点
在点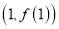 处的切线方程;
处的切线方程;(Ⅱ)讨论函数
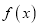 的单调性;
的单调性;(Ⅲ)若
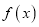 存在两个极值点
存在两个极值点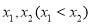 ,求
,求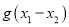 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设各项均为正数的数列
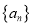 的前n项和为
的前n项和为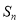 ,满足
,满足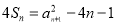 ,且
,且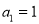 ,公比大于1的等比数列
,公比大于1的等比数列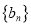 满足
满足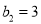 ,
, 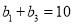 .
.(1)求证数列
 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;(2)若
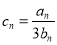 ,求数列
,求数列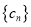 的前n项和
的前n项和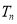 ;
;(3)在(2)的条件下,若
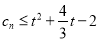 对一切正整数n恒成立,求实数t的取值范围.
对一切正整数n恒成立,求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前n项和
的前n项和 ,
,  是等差数列,且
是等差数列,且 .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)令
 .求数列
.求数列 的前n项和
的前n项和 .
.
相关试题

