【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
参考答案:
【答案】(1)详见解析;(2) 详见解析;(3) 详见解析;(4) 详见解析.
【解析】试题分析:(1)将x=-1,0,1,2,3代入解析式,求出y值,即可得函数的值域;(2) (x-1)2+1≥1,则值域为{y|y≥1};(3)分离常数,可得![]() ,因为x≠1,所以y≠5;(4)令
,因为x≠1,所以y≠5;(4)令![]() ,则x=t2-1(t≥0),代入原函数可得关于t的二次函数,通过配方法求出函数的值域.
,则x=t2-1(t≥0),代入原函数可得关于t的二次函数,通过配方法求出函数的值域.
试题解析:
(1)函数的定义域为{-1,0,1,2,3},则f(-1)=[(-1)-1]2+1=5,同理可得f(0)=2,f(1)=1,f(2)=2,f(3)=5,所以函数的值域为{1,2,5}.
(2)函数的定义域为R,因为(x-1)2+1≥1,所以函数的值域为{y|y≥1}.
(3)函数的定义域是{x|x≠1},y=![]() =5+
=5+![]() ,所以函数的值域为{y|y≠5}.
,所以函数的值域为{y|y≠5}.
(4)要使函数式有意义,需x+1≥0,即x≥-1,故函数的定义域是{x|x≥-1}.
设t=![]() ,则x=t2-1(t≥0),于是f(t)=t2-1-t=
,则x=t2-1(t≥0),于是f(t)=t2-1-t=![]() 2-
2-![]() .
.
又因为t≥0,故f(t)≥-![]() .所以函数的值域是
.所以函数的值域是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
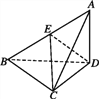
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(2)+f
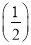 ,f(3)+f
,f(3)+f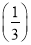 的值;
的值;(2)求证:f(x)+f
 是定值;
是定值;(3)求f(2)+f
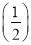 +f(3)+f
+f(3)+f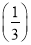 +…+
+…+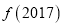 +f
+f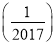 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0. 若B的坐标为(1,2),求△ABC三边所在直线方程及点C坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至
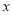 元,则本年度新增用电量
元,则本年度新增用电量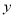 (亿千瓦时)与
(亿千瓦时)与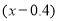 元成反比例.又当
元成反比例.又当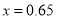 时,
时,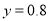 .
.(1)求
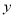 与
与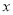 之间的函数关系式;
之间的函数关系式;(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益
 用电量
用电量 (实际电价-成本价)]
(实际电价-成本价)] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+1,x∈R.
(1)分别计算f(1)-f(-1),f(2)-f(-2),f(3)-f(-3)的值;
(2)由(1)你发现了什么结论?并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
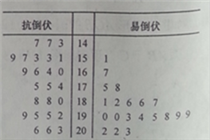 (1)完成列
(1)完成列 联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?

相关试题

