【题目】设a>0且a≠1,函数f(x)=![]() x2-(a+1)x+alnx.
x2-(a+1)x+alnx.
(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;
(2)求函数f(x)的极值点.
参考答案:
【答案】(1)![]() .(2) 见解析.
.(2) 见解析.
【解析】试题分析:(1)由已知中函数 ![]() ,根据a=2,我们易求出f(3)及f′(3)的值,代入即可得到切线的斜率k=f′(3).
,根据a=2,我们易求出f(3)及f′(3)的值,代入即可得到切线的斜率k=f′(3).
(2)由已知我们易求出函数的导函数,令导函数值为0,我们则求出导函数的零点,根据m>0,我们可将函数的定义域分成若干个区间,分别在每个区间上讨论导函数的符号,即可得到函数函数f(x)的极值点.
试题解析:
(1)由已知得x>0.
当a=2时,f′(x)=x-3+![]() ,f′(3)=,
,f′(3)=,
所以曲线y=f(x)在(3,f(3))处切线的斜率为.
(2)f′(x)=x-(a+1)+![]()
=![]() =
=![]() .
.
由f′(x)=0,得x=1或x=a.
①当0<a<1时,
当x∈(0,a)时,f′(x)>0,函数f(x)单调递增;
当x∈(a,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,f′(x)>0,函数f(x)单调递增.
此时x=a时f(x)的极大值点,x=1是f(x)的极小值点.
②当a>1时,
当x∈(0,1)时,f′(x)>0,函数f(x)单调递增;
当x∈(1,a)时,f′(x)<0,函数f(x)单调递减;
当x∈(a,+∞)时,f′(x)>0,函数f(x)单调递增.
此时x=1是f(x)的极大值点,x=a是f(x)的极小值点.
综上,当0<a<1时,x=a是f(x)的极大值点,x=1是f(x)的极小值点;
当a>1时,x=1是f(x)的极大值点,x=a是f(x)的极小值点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3+2x2﹣ax+1在区间(﹣1,1)上恰有一个极值点,则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是首项为19,公差为-2的等差数列,Sn为{an}的前n项和.
(1)求通项an及Sn;
(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)已知不等式ax2-3x+6>4的解集为{x|x<1或x>b},
(1)求a,b;
(2)解不等式ax2-(ac+b)x+bc<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
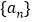 的前n项和为
的前n项和为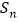 ,并且满足
,并且满足 ,
, .
.(1)求数列
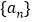 的通项公式;
的通项公式;(2)若
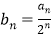 ,数列
,数列 的前n项和为
的前n项和为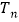 ,求
,求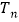 ;
;(3)在(2)的条件下,是否存在常数
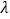 ,使得数列
,使得数列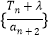 为等比数列?若存在,试求出
为等比数列?若存在,试求出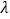 ;若不存在,说明理由.
;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 是
是  或
或 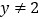 的充分不必要条件
的充分不必要条件
B.若命题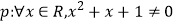 ,则
,则 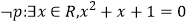
C.线性相关系数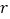 的绝对值越接近1,表示两变量的相关性越强
的绝对值越接近1,表示两变量的相关性越强
D.用频率分布直方图估计平均数,可以用每个小矩形的高乘以底边中点横坐标之和 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
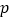 :“函数
:“函数 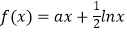 在区间
在区间 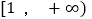 上单调递减”;命题
上单调递减”;命题 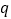 :“存在正数
:“存在正数 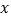 ,使得
,使得 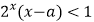 成立”,若
成立”,若 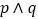 为真命题,则
为真命题,则 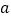 的取值范围是( )
的取值范围是( )
A.
B.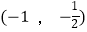
C.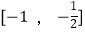
D.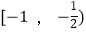
相关试题

