【题目】定义在(0,+∞)上的函数f(x),如果对任意x∈(0,+∞),恒有f(kx)=kf(x),(k≥2,k∈N+)成立,则称f(x)为k阶缩放函数.
(1)已知函数f(x)为二阶缩放函数,且当x∈(1,2]时,f(x)=1+ ![]() x,求f(2
x,求f(2 ![]() )的值;
)的值;
(2)已知函数f(x)为二阶缩放函数,且当x∈(1,2]时,f(x)= ![]() ,求证:函数y=f(x)﹣x在(1,+∞)上无零点;
,求证:函数y=f(x)﹣x在(1,+∞)上无零点;
(3)已知函数f(x)为k阶缩放函数,且当x∈(1,k]时,f(x)的取值范围是[0,1),求f(x)在(0,kn+1](n∈N)上的取值范围.
参考答案:
【答案】
(1)解:由 ![]() ∈(1,2]得,f(
∈(1,2]得,f( ![]() )=1+1+
)=1+1+ ![]()
![]() =
= ![]()
由题中条件得f(2 ![]() )=2f(
)=2f( ![]() )=2×
)=2× ![]() =1
=1
(2)解:当x∈(2i,2i+1](i=0,1,2)时, ![]() ∈(1,2],依题意可得:f(x)=2f(
∈(1,2],依题意可得:f(x)=2f( ![]() )=22f(
)=22f( ![]() )=…=2if(
)=…=2if( ![]() )=2i
)=2i ![]() =
= ![]()
方程f(x)﹣x=0 ![]() =xx=0或x=2i,0与2i均不属于(2i,2i+1]((i=0,1,2))当x∈(2i,2i+1]((i=0,1,2))时,方程f(x)﹣x=0无实数解.
=xx=0或x=2i,0与2i均不属于(2i,2i+1]((i=0,1,2))当x∈(2i,2i+1]((i=0,1,2))时,方程f(x)﹣x=0无实数解.
注意到(1,+∞)=(20,21]∪(21,22]∪(22,23)∪…,所以函数y=f(x)﹣x在(1,+∞)上无零点
(3)解:当x∈(kj,kj+1],j∈Z时,有 ![]() ∈(1,k],依题意可得:f(x)=kf(
∈(1,k],依题意可得:f(x)=kf( ![]() )=k2f(
)=k2f( ![]() )=…=kjf(
)=…=kjf( ![]() )
)
当x∈(1,k]时,f(x)的取值范围是[0,1)
所以当x∈(kj,kj+1],j∈Z时,f(x)的取值范围是[0,kj).
由于(0,kn+1]=(kn,kn+1]∪(kn﹣1,kn]∪…∪(k0,k]∪(k﹣1,k0]∪
所以函数f(x)在(0,kn+1](n∈N)上的取值范围是:[0,kn)∪[0,kn﹣1)∪…∪[0,k0)∪[0,k﹣1)∪…=[0,kn)
【解析】(1)根据二阶缩放函数的定义,直接代入进行求值即可;(2)根据函数零点的定义和性质判断函数y=f(x)﹣x在(1,+∞)上无零点;(3)根据k阶缩放函数成立的条件建立条件关系即可求出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】几位同学在研究函数

 时,给出了下面几个结论:
时,给出了下面几个结论:①
 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是 ;
;②若
 ,则一定有
,则一定有 ;
; ③函数
 的值域为
的值域为 ;
;④若规定
 ,
, ,则
,则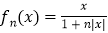 对任意
对任意 恒成立.
恒成立.上述结论中正确的是____
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 若对任意的正整数n,总存在正整数m,使得Sn=am , 则称{an}是“H数列”.
(1)若数列{an}的前n项和为Sn=2n(n∈N*),证明:{an}是“H数列”;
(2)设{an}是等差数列,其首项a1=1,公差d<0,若{an}是“H数列”,求d的值;
(3)证明:对任意的等差数列{an},总存在两个“H数列”{bn}和{cn},使得an=bn+cn(n∈N*)成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知函数f(x)=

(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数x,记[x]表示不超过x的最大整数,如[3.14]=3,[﹣0.25]=﹣1.若存在实数t,使得[t]=1,[t2]=2,[t3]=3…[tt]=n同时成立,则正整数n的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
. 当
当 时,试判断函数
时,试判断函数 在区间
在区间 上的单调性,并证明;
上的单调性,并证明; 若不等式
若不等式 在
在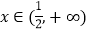 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△A1B1C1的三内角余弦值分别等于△A2B2C2三内角的正弦值,那么两个三角形六个内角中的最大值为 .
相关试题

