【题目】已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: ![]() =3n2an+
=3n2an+![]() ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
参考答案:
【答案】(1)3(2)![]()
【解析】试题分析:(1)数列{an}是等差数列,故可从特殊情形出发:先求出a2=12-2a,a3=3+2a.再利用a1+a3=2a2,解得a=3.最后验证.(2)先由通项与和项关系,将已知条件转化为递推关系:an+1+an=6n+3,(n≥2).an+2-an=6,(n≥2),即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列,要使数列{an}是递增数列,须有a1<a2![]() ,解得
,解得![]() <a<
<a<![]() .
.
试题解析:(1)在![]() =3n2an+
=3n2an+![]() 中分别令n=2,n=3,及a1=a得
中分别令n=2,n=3,及a1=a得
(a+a2)2=12a2+a2,(a+a2+a3)2=27a3+(a+a2)2,
因an≠0,所以a2=12-2a,a3=3+2a. 2分
因数列{an}是等差数列,所以a1+a3=2a2,即2(12-2a)=a+3+2a,解得a=3. 4分
经检验a=3时,an=3n,Sn=![]() ,Sn-1=
,Sn-1=![]() 满足
满足![]() =3n2an+
=3n2an+![]()
(2)由![]() =3n2an+
=3n2an+![]() ,得
,得![]() -
-![]() =3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
=3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
即(Sn+Sn-1)an=3n2an,因为an≠0,所以Sn+Sn-1=3n2,(n≥2),① 6分
所以Sn+1+Sn=3(n+1)2,②
②-①,得an+1+an=6n+3,(n≥2).③ 8分
所以an+2+an+1=6n+9,④
④-③,得an+2-an=6,(n≥2)
即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列, 10分
因为a2=12-2a,a3=3+2a.
所以an=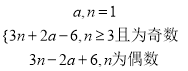 12分
12分
要使数列{an}是递增数列,须有
a1<a2,且当n为大于或等于3的奇数时,an<an+1,且当n为偶数时,an<an+1,
即a<12-2a,
3n+2a-6<3(n+1)-2a+6(n为大于或等于3的奇数),
3n-2a+6<3(n+1)+2a-6(n为偶数),
解得![]() <a<
<a<![]() .所以M=
.所以M=![]() ,当a∈M时,数列{an}是递增数列. 16分
,当a∈M时,数列{an}是递增数列. 16分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
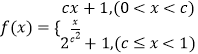 ,且
,且 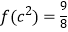 .
.
(1)求实数c的值;
(2)解不等式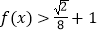 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
在正三棱柱
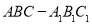 中,点
中,点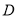 是
是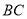 的中点,
的中点, .
.(1)求证:
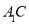 ∥平面
∥平面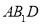 ;
;(2)试在棱
 上找一点
上找一点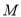 ,使
,使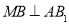 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
如图,2015年春节,摄影爱好者
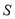 在某公园
在某公园 处,发现正前方
处,发现正前方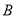 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端 的仰角和立柱底部
的仰角和立柱底部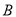 的俯角均为
的俯角均为 ,已知
,已知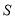 的身高约为
的身高约为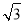 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按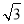 米处理)
米处理)
(1)求摄影者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆
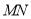 绕中点
绕中点 在
在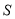 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C=
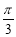 ,acosA=bcosB.
,acosA=bcosB.(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】若
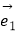 ,
, 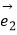 ,
, 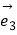 为同一平面内互不共线的三个单位向量,并满足
为同一平面内互不共线的三个单位向量,并满足 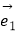 +
+ 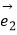 +
+ 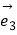 =
= 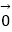 ,且向量
,且向量 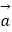 =x
=x 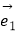 +
+ 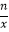
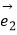 +(x+
+(x+ 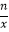 )
) 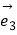 (x∈R,x≠0,n∈N+).
(x∈R,x≠0,n∈N+).
(1)求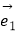 与
与 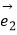 所成角的大小;
所成角的大小;
(2)记f(x)=|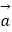 |,试求f(x)的单调区间及最小值.
|,试求f(x)的单调区间及最小值.
相关试题

