【题目】(1)已知直线方程为(2+m)x+(1-2m)y+4-3m=0,求证:不论m为何实数,此直线必过定点;
(2)过这定点引一直线,使它夹在两坐标轴间的线段被这点平分,求这条直线的方程.
参考答案:
【答案】(1)证明见解析;(2)2x+y+4=0
【解析】试题分析:(1)直线方程整理得m(x-2y-3)+2x+y+4=0,所以![]() ,求出定点;(2)由(-1,-2)是线段AB的中点,得到A(-2,0),B(0,-4),写出直线方程。
,求出定点;(2)由(-1,-2)是线段AB的中点,得到A(-2,0),B(0,-4),写出直线方程。
试题解析:
(1)证明:直线方程可写为m(x-2y-3)+2x+y+4=0,
由![]() ,得
,得![]() ,
,
∴点(-1,-2)适合方程(2+m)x+(1-2m)·y+4-3m=0,
因此,直线(2+m)x+(1-2m)y+4-3m=0过定点(-1,-2).
(2)设过点(-1,-2)所引的直线与x轴、y轴分别交于A(a,0),B(0,b)点,
∵(-1,-2)是线段AB的中点,
∴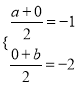 ,解得
,解得![]()
∴所求直线方程为![]() ,即2x+y+4=0.
,即2x+y+4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某医疗研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线.

(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4 μg时治疗疾病有效,假若某病人一天中第一次服药为上午7:00,问:一天中怎样安排服药时间(共4次)效果最佳?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga(x+2)-1(a>0,且a≠1),g(x)=
 x-1.
x-1.(1)若函数y=f(x)的图象恒过定点A,求点A的坐标;
(2)若函数F(x)=f(x)-g(x)的图象过点
 ,试证明函数F(x)在x∈(1,2)上有唯一零点.
,试证明函数F(x)在x∈(1,2)上有唯一零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条直线l1:2x-y+a =" 0" (a>0),直线l2:-4x+2y+1 = 0和直线l3:x+y-1= 0,且l1与l2的距离是
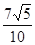 .
.(1)求a的值;
(2)能否找到一点P,使得P点同时满足下列三个条 件:
①P是第一象限的点;
②P 点到l1的距离是P点到l2的距离的
 ;
;③P点到l1的距离与P点到l3的距离之比是
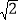 ∶
∶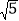 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x-1+
 x2-2,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1).
x2-2,试利用基本初等函数的图象,判断f(x)有几个零点,并利用零点存在性定理确定各零点所在的区间(各区间长度不超过1). -
科目: 来源: 题型:
查看答案和解析>>【题目】若有穷数列
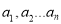 (
(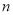 是正整数),满足
是正整数),满足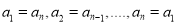 即
即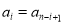 (
(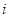 是正整数,且
是正整数,且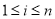 ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列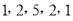 与数列
与数列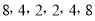 都是“对称数列”.
都是“对称数列”. (1)已知数列
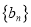 是项数为9的对称数列,且
是项数为9的对称数列,且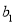 ,
,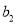 ,
,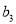 ,
,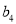 ,
,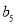 成等差数列,
成等差数列, 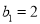 ,
, 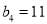 ,试求
,试求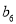 ,
, 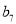 ,
, 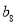 ,
, 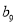 ,并求前9项和
,并求前9项和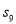 .
.(2)若
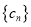 是项数为
是项数为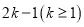 的对称数列,且
的对称数列,且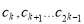 构成首项为31,公差为
构成首项为31,公差为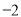 的等差数列,数列
的等差数列,数列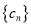 前
前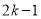 项和为
项和为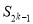 ,则当
,则当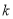 为何值时,
为何值时, 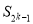 取到最大值?最大值为多少?
取到最大值?最大值为多少?(3)设
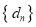 是
是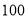 项的“对称数列”,其中
项的“对称数列”,其中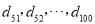 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求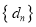 前
前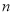 项的和
项的和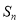
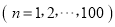 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
相关试题

