【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若函数![]() 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(1)![]() .(2)详见解析.
.(2)详见解析.
【解析】试题分析:(Ⅰ)首先求得函数的定义域与导函数,然后结合判别式判断导函数的符号,得到函数的单调性,从而求得![]() 的取值范围;(Ⅱ)首先将问题转化为
的取值范围;(Ⅱ)首先将问题转化为![]() 有两个不等的实根
有两个不等的实根![]() ,
, ![]() ,由此得到
,由此得到![]() 的范围,从而得到
的范围,从而得到![]() ,
, ![]() 的范围,然后根据
的范围,然后根据![]() 的表达式构造新函数,由此通过求导研究新函数的单调性使问题得证.
的表达式构造新函数,由此通过求导研究新函数的单调性使问题得证.
试题解析:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,
由题意![]() ,
,
![]() .
.
①若![]() ,即
,即![]() ,则
,则![]() 恒成立,
恒成立,
则![]() 在
在![]() 上为单调减函数;
上为单调减函数;
②若![]() ,即
,即![]() ,方程
,方程![]() 的两根为
的两根为![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 单调递增,不符合题意.
单调递增,不符合题意.
综上,若函数![]() 为定义域上的单调函数,则实数
为定义域上的单调函数,则实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)因为函数![]() 有两个极值点,所以
有两个极值点,所以![]() 在
在![]() 上有两个不等的实根,
上有两个不等的实根,
即![]() 在
在![]() 有两个不等的实根
有两个不等的实根![]() ,
, ![]() ,
,
于是![]() ,
, 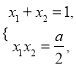 且满足
且满足![]() ,
, ![]() ,
,
![]() ,
,
同理可得![]() .
.
![]() ,
,
令![]() ,
, ![]() .
.
![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又![]() 时,
时, ![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,得证.
,得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在等式
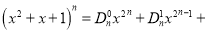
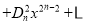
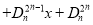
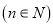 中,把
中,把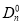 ,
, 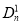 ,
, 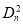 ,…,
,…, 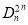 叫做三项式的
叫做三项式的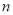 次系数列(如三项式的1次系数列是1,1,1).
次系数列(如三项式的1次系数列是1,1,1).(1)填空:三项式的2次系数列是_______________;
三项式的3次系数列是_______________;
(2)由杨辉三角数阵表可以得到二项式系数的性质
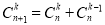 ,类似的请用三项式
,类似的请用三项式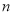 次系数列中的系数表示
次系数列中的系数表示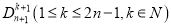 (无须证明);
(无须证明);(3)求
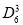 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中,表示同一函数的是( )
A.f(x)=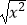 ,g(x)=(
,g(x)=( 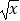 )2
)2
B.f(x)=(x﹣1)0 , g(x)=1
C.f(x)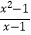 ,g(x)=x+1
,g(x)=x+1
D.f(x)=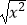 ,g(t)=|t|
,g(t)=|t| -
科目: 来源: 题型:
查看答案和解析>>【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有
 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程
 中,当解释变量
中,当解释变量 每增加一个单位时,预报变量
每增加一个单位时,预报变量 平均增加0.2个单位;
平均增加0.2个单位;④对分类变量
 与
与 ,它们的随机变量
,它们的随机变量 的观测值
的观测值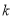 来说,
来说,  越小,“
越小,“ 与
与 有关系”的把握程度越大.
有关系”的把握程度越大.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 为平行四边形,
为平行四边形, 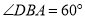 ,
, 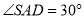 ,
, 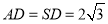 ,
, 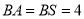 .
. 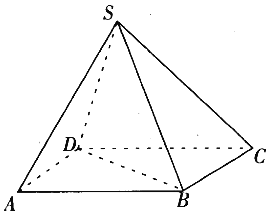
(Ⅰ)证明:
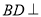 平面
平面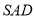 ;
;(Ⅱ)求二面角
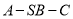 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2x+1的定义域为[1,5],则函数f(2x﹣3)的定义域为( )
A.[1,5]
B.[3,11]
C.[3,7]
D.[2,4] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为
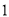 ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )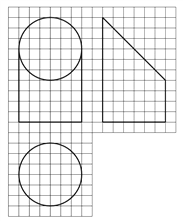
A.
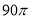 B.
B. 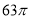 C.
C. 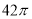 D.
D. 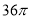
相关试题

