【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
参考答案:
【答案】
(1)解:设等差数列{an}的公差为d,
∵a1+1,a2+1,a4+1成等比数列,∴ ![]() =(a1+1)(a4+1),
=(a1+1)(a4+1),
又S3=﹣15,∴ ![]() =﹣15,∴a2=﹣5.
=﹣15,∴a2=﹣5.
∴(﹣5+1)2=(﹣5﹣d+1)(﹣5+2d+1),解得d=0或d=﹣2.
d=0时,公比为1,舍去.
∴d=﹣2.
∴an=a2﹣2(n﹣2)=﹣5﹣2(n﹣2)=﹣2n﹣1
(2)解:由(1)可得:Sn= ![]() =﹣n2﹣2n.
=﹣n2﹣2n.
∴bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴数列{bn}的前n项和Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
=﹣ ![]()
=﹣ ![]() +
+ ![]()
【解析】(1)设等差数列{an}的公差为d,根据a1+1,a2+1,a4+1成等比数列,可得 ![]() =(a1+1)(a4+1),又S3=﹣15,可得
=(a1+1)(a4+1),又S3=﹣15,可得 ![]() =3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn=
=3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,利用“裂项求和”即可得出.
,利用“裂项求和”即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
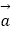 =(cosx+sinx,1),
=(cosx+sinx,1), 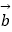 =(cosx+sinx,﹣1)函数g(x)=4
=(cosx+sinx,﹣1)函数g(x)=4 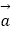
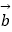 .
.
(1)求函数g(x)在[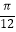 ,
,  ]上的值域;
]上的值域;
(2)若x∈[0,2016π],求满足g(x)=0的实数x的个数;
(3)求证:对任意λ>0,都存在μ>0,使g(x)+x﹣4<0对x∈(﹣∞,λμ)恒成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: ①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′﹣DEF的体积最大值为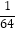 a3;
a3;
④动点A′在平面ABC上的射影在线段AF上;
⑤二面角A′﹣DE﹣F大小的范围是[0, ].
].
其中正确的命题是(写出所有正确命题的编号)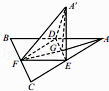
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程
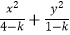 =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin(x﹣
 )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移  个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.
B.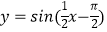
C.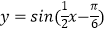
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x+sin|x|,x∈[﹣π,π]的大致图象是( )
A.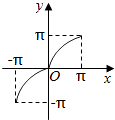
B.
C.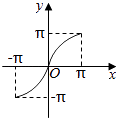
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平行四边形ABB1A1中,∠ABB1=60°,AB=4,AA1=2,C,C1分别为AB,A1B1的中点,现把平行四边形ABB1A1沿CC1折起如图2所示,连接B1C,B1A,B1A1 .
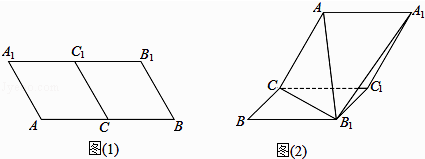
(1)求证:AB1⊥CC1;
(2)若AB1=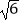 ,求二面角C﹣AB1﹣A1的余弦值.
,求二面角C﹣AB1﹣A1的余弦值.
相关试题

