【题目】某保险公司针对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金.保险公司把企业的所有岗位共分为A、B、C三类工种,从事三类工种的人数分布比例如图,根据历史数据统计出三类工种的赔付频率如下表(并以此估计赔付频率).
工种类别 | A | B | C |
赔付频率 |
|
|
|
对于A、B、C三类工种职工每人每年保费分别为a元,a元,b元,出险后的赔偿金额分别为100万元,100万元,50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(Ⅰ)若保险公司要求利润的期望不低于保费的20%,试确定保费a、b所要满足的条件;
(Ⅱ)现有如下两个方案供企业选择;
方案1:企业不与保险公司合作,企业自行拿出与保险提供的等额的赔偿金额赔付给出险职工;
方案2:企业与保险公司合作,企业负责职工保费的60%,职工个人负责保费的40%,出险后赔偿金由保险公司赔付.
若企业选择翻翻2的支出(不包括职工支出)低于选择方案1的支出期望,求保费a、b所要满足的条件,并判断企业是否可与保险公司合作.(若企业选择方案2的支出低于选择方案1的支出期望,且与(Ⅰ)中保险公司所提条件不矛盾,则企业可与保险公司合作.)
参考答案:
【答案】解:(Ⅰ)设工种A,B,C职工的每份保单保险公司的效益为随机变量X,Y,Z, 则随机变量X的分布列为:
X | a | a﹣100×104 |
P |
|
|
随机变量Y的分布列为:
Y | a | a﹣100×104 |
P |
|
|
随机变量Z的分布列为:
Z | b | b﹣50×104 |
P |
|
|
保险公司期望收益为 ![]() =a﹣10,
=a﹣10,![]() =a﹣20,
=a﹣20,![]() =b﹣50;
=b﹣50;
根据要求(a﹣10)×20000×0.6+(a﹣20)×20000×0.3+(b﹣50)×20000×0.1﹣10×104
≥(a×20000×0.6+a×20000×0.3+b×20000×0.1)×0.2,
解得9a+b≥275,
所以每张保单的保费需要满足9a+b≥275元;
(Ⅱ)若该企业不与保险公司合作,则安全支出,
即赔偿金的期望值为
20000×0.6× ![]() ×100×104+0.3×
×100×104+0.3× ![]() ×100×104+0.1×
×100×104+0.1× ![]() ×50×104=17×20000;
×50×104=17×20000;
若该企业与保险公司合作,则安全支出,
即保费为20000×(0.6×a+0.3×a+0.1×b)×0.6=(0.9×a+0.1×b)×0.6×20000;
解得9a+b<283.33,
结果与(Ⅰ)不冲突,所以企业有可能与保险公司合作
【解析】(Ⅰ)设工种A,B,C职工的每份保单保险公司的效益为随机变量X,Y,Z,写出随机变量X、Y、Z的分布列,计算保险公司期望收益EX、EY、EZ;根据要求列出不等式,求出a、b满足的条件;(Ⅱ)计算企业不与保险公司合作时安全支出(即赔偿金的期望值),以及企业与保险公司合作的安全支出(即保费),比较大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤
 (x+2)2成立.
(x+2)2成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-
 x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y= 的上方,求实数m的取值范围.
的上方,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在三棱柱ABC﹣A1B1C1中,AA1B1B为正方形,BB1C1C为菱形,B1C⊥AC1 .
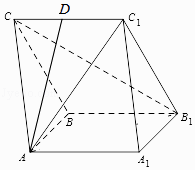
(Ⅰ)求证:平面AA1B1B⊥平面BB1C1C;
(Ⅱ)若D是CC1中点,∠ADB是二面角A﹣CC1﹣B的平面角,求直线AC1与平面ABC所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线C1:y=
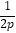 x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2: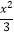 -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p=( ).A.
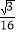 B.
B.  C.
C. 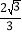 D.
D. 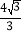
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+y2=16,F(﹣1,0),M是圆C上的一个动点,线段MF的垂直平分线与线段MC相交于点P.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)记点P的轨迹为C1 , A、B是直线x=﹣2上的两点,满足AF⊥BF,曲线C1与过A,B的两条切线(异于x=﹣2)交于点Q,求四边形AQBF面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=xln(ax+1)(a≠0).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若a>0且满足:对x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤ln3﹣ln2,试比较ea﹣1与 的大小,并证明.
的大小,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】曲线
 是平面内到定点
是平面内到定点 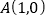 的距离与到定直线
的距离与到定直线  的距离之和为
的距离之和为  的动点
的动点  的轨迹.则曲线
的轨迹.则曲线  与
与 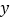 轴交点的坐标是________________;又已知点
轴交点的坐标是________________;又已知点  (
(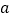 为常数),那么
为常数),那么 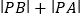 的最小值
的最小值  ________________.
________________.
相关试题

