【题目】已知圆![]() 及直线
及直线![]() ,直线
,直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(![]() )求实数
)求实数![]() 的值.
的值.
(![]() )求过点
)求过点![]() 并与圆
并与圆![]() 相切的切线方程.
相切的切线方程.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
试题分析:(1)根据圆的方程找出圆心坐标与圆的半径,然后利用点到直线的距离公式表示出圆心到直线![]() 的距离
的距离![]() ,然后根据垂径定理得到弦心距,弦的一半及圆的半径成直角三角形,利用勾股对了列出关于
,然后根据垂径定理得到弦心距,弦的一半及圆的半径成直角三角形,利用勾股对了列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,然后由
的值,然后由![]() 大于0,得到满足题意
大于0,得到满足题意![]() 的值;(2)把(1)求出
的值;(2)把(1)求出![]() 的值代入圆的方程中确定出圆的方程,即可得到圆心的坐标,并判断得到已知点在圆外,分两种情况:当切线的斜率不存在时,得到
的值代入圆的方程中确定出圆的方程,即可得到圆心的坐标,并判断得到已知点在圆外,分两种情况:当切线的斜率不存在时,得到![]() 为圆的切线;当切线的斜率存在时,设切线的斜率为
为圆的切线;当切线的斜率存在时,设切线的斜率为![]() ,由
,由![]() 和设出的
和设出的![]() 写出切线的方程,根据直线与圆相切时圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到切线的距离
写出切线的方程,根据直线与圆相切时圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到切线的距离![]() ,让
,让![]() 等于圆的半径即可列出关于
等于圆的半径即可列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,把
的值,把![]() 的值代入所设的切线方程即可确定出切线的方程.
的值代入所设的切线方程即可确定出切线的方程.
试题解析:(![]() )根据题意可得圆心
)根据题意可得圆心![]() ,半径
,半径![]() ,则圆心到直线
,则圆心到直线![]() 的距离
的距离![]() ,
,
由勾股定理可以知道![]() ,代入化简得
,代入化简得![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,
,
所以![]() .
.
(![]() )由(
)由(![]() )知圆
)知圆![]() ,圆心为
,圆心为![]() ,半径
,半径![]() ,
,
点![]() 到圆心的距离为
到圆心的距离为![]() ,故点
,故点![]() 在圆外,
在圆外,
当切线方程的斜率存在时,设方程为![]() ,则圆心到切线的距离
,则圆心到切线的距离![]() ,
,
化简得:![]() ,故
,故![]() .
.
∴切线方程为![]() ,
,
即![]() ,
,
当切线方程斜率不存在时,直线方程为![]() 与圆相切,
与圆相切,
综上,过点![]() 并与圆相切的切线方程为
并与圆相切的切线方程为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
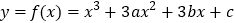 在
在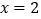 处有极值,且其图像在
处有极值,且其图像在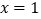 处的切线与直线
处的切线与直线 平行.
平行.(I).求函数的单调区间;
(II).求函数的极大值与极小值的差;
(III).若
 时,
时,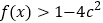 恒成立,求实数
恒成立,求实数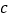 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 +
+ =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,
 )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
 ,
, ,
, ,将
,将 沿矩形的对角线
沿矩形的对角线 所在的直线进行翻折,在翻折过程中,则( ).
所在的直线进行翻折,在翻折过程中,则( ).A. 当
 时,存在某个位置,使得
时,存在某个位置,使得
B. 当
 时,存在某个位置,使得
时,存在某个位置,使得
C. 当
 时,存在某个位置,使得
时,存在某个位置,使得
D.
 时,都不存在某个位置,使得
时,都不存在某个位置,使得
-
科目: 来源: 题型:
查看答案和解析>>【题目】户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
喜欢户外运动
不喜欢户外运动
合计
男性
5
女性
10
合计
50
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是
 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由;
(3)经进一步调查发现,在喜欢户外运动的10名女性员工中,有4人还喜欢瑜伽.若从喜欢户外运动的10位女性员工中任选3人,记ξ表示抽到喜欢瑜伽的人数,求ξ的分布列和数学期望.
下面的临界值表仅供参考:P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:
 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
 中,侧棱垂直于底面,
中,侧棱垂直于底面,  分别是
分别是 的中点.
的中点.(1)求证: 平面
 平面
平面 ;
;(2)求证:
 平面
平面 ;
;(3)求三棱锥
 体积.
体积.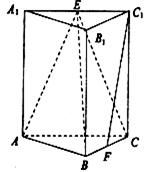
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥B﹣ACDE中,AE⊥平面ABC,CD∥AE,∠ABC=3∠BAC=90°,BF⊥AC于F,AC=4CD=4,AE=3.

(1)求证:BE⊥DF;
(2)求二面角B﹣DE﹣F的平面角的余弦值.
相关试题

