【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记事件![]() 表示“
表示“![]() ”,求事件
”,求事件![]() 的概率;
的概率;
(2)在区间![]() 内任取两个实数
内任取两个实数![]() ,
,![]() ,求“事件
,求“事件![]() 恒成立”的概率.
恒成立”的概率.
参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)从袋子中不放回地随机抽取2个球,共有基本事件12个,其中“a+b=2”为事件A的基本事件有4个,故可求概率.(2)记“x2+y2>(a﹣b)2恒成立”为事件B,则事件B等价于“x2+y2>4恒成立,(x,y)可以看成平面中的点,确定全部结果所构成的区域,事件B构成的区域,利用几何概型可求得结论.
(1)两次不放回抽取小球的所有基本事件为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共12个,事件
,共12个,事件![]() 包含的基本事件为
包含的基本事件为![]() ,
,![]() ,
,![]() ,
,![]() ,共4个.
,共4个.
所以![]() .
.
(2)记“![]() 恒成立”为事件
恒成立”为事件![]() ,
,
则事件![]() 等价于“
等价于“![]() ”.
”.
![]() 可以看成平面中的点,
可以看成平面中的点,
则全部结果所构成的区域![]() ,
,
而事件![]() 所构成的区域
所构成的区域![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是函数f(x)=
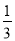 ax3-
ax3-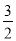 x2+(a+1)x+5的一个极值点.
x2+(a+1)x+5的一个极值点.(1)求函数f(x)的解析式;
(2)若曲线y=f(x)与直线y=2x+m有三个交点,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
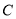 :
: 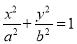 (
(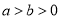 )的左右焦点分别为
)的左右焦点分别为 ,
, 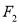 ,下顶点为
,下顶点为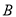 ,直线
,直线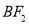 的方程为
的方程为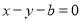 .
.(Ⅰ)求椭圆
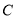 的离心率;
的离心率;(Ⅱ)设
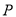 为椭圆上异于其顶点的一点,
为椭圆上异于其顶点的一点, 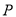 到直线
到直线 的距离为
的距离为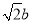 ,且三角形
,且三角形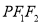 的面积为
的面积为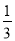 .
.(1)求椭圆
 的方程;
的方程;(2)若斜率为
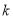 的直线
的直线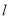 与椭圆
与椭圆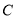 相切,过焦点
相切,过焦点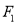 ,
, 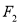 分别作
分别作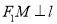 ,
, 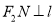 ,垂足分别为
,垂足分别为 ,
, 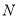 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球2个.从袋子中不放回地随机抽取小球两个,每次抽取一个球,记第一次取出的小球标号为
 ,第二次取出的小球标号为
,第二次取出的小球标号为 .
.(1)记事件
 表示“
表示“ ”,求事件
”,求事件 的概率;
的概率;(2)在区间
 内任取两个实数
内任取两个实数 ,
, ,求“事件
,求“事件 恒成立”的概率.
恒成立”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个古典型(或几何概型)中,若两个不同随机事件
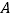 、
、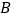 概率相等,则称
概率相等,则称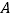 和
和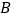 是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.①在同一个古典概型中,所有的基本事件之间都是“等概率事件”;
②若一个古典概型的事件总数为大于2的质数,则在这个古典概型中除基本事件外没有其他“等概率事件”;③因为所有必然事件的概率都是1,所以任意两个必然事件是“等概率事件”;
④随机同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=-
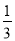 x3+x2+(m2-1)x(x∈R),其中m>0.
x3+x2+(m2-1)x(x∈R),其中m>0.(1)当m=1时,求曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2sin(2x﹣
 ),x∈R.
),x∈R. 
(1)在给定的平面直角坐标系中,画函数f(x)=2sin(2x﹣ ),x∈[0,π]的简图;
),x∈[0,π]的简图;
(2)求f(x)=2sin(2x﹣ ),x∈[﹣π,0]的单调增区间;
),x∈[﹣π,0]的单调增区间;
(3)函数g(x)=2cos2x的图象只经过怎样的平移变换就可得到f(x)=2sin(2x﹣ ),x∈R的图象?
),x∈R的图象?
相关试题

