【题目】在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,已知
,已知![]() .
.
(1)求证:![]() 成等差数列;
成等差数列;
(2)若![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() .
.
参考答案:
【答案】(1)证明见解析;(2)4.
【解析】试题分析:
(1)结合题意首先利用正弦定理边化角,结合两角和差正余弦公式进行化简,然后再角化边即可证得题中的结论;
(2)由余弦定理得到关于边c的方程,解方程即可求得边长的值.
试题解析:
(1)∵b(1+cosC)=c(2-cosB),
∴由正弦定理可得:sinB+sinBcosC=2sinC-sinCcosB,可得:sinBcosC+sinCcosB+sinB=2sinC,
∴sinA+sinB=2sinC,
∴a+b=2c,即a,c,b成等差数列;
(2)∵C=![]() ,△ABC的面积为4
,△ABC的面积为4![]() =
=![]() absinC=
absinC=![]() ab,
ab,
∴ab=16,
∵由余弦定理可得:c2=a2+b2-2abcosC=a2+b2-ab=(a+b)2-3ab,
∵a+b=2c,
∴可得:c2=4c2-3×16,解得:c=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
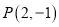 ,求:
,求:(Ⅰ)过
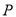 点与原点距离为2的直线
点与原点距离为2的直线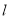 的方程;
的方程;(Ⅱ)过
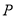 点与原点距离最大的直线
点与原点距离最大的直线 的方程,最大距离是多少?
的方程,最大距离是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗
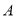 原料1千克、
原料1千克、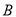 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗 原料2千克,
原料2千克, 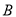 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线:
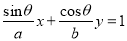 (
(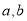 为给定的正常数,
为给定的正常数, 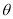 为参数,
为参数, 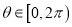 )构成的集合为
)构成的集合为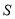 ,给出下列命题:
,给出下列命题:①当
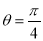 时,
时, 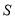 中直线的斜率为
中直线的斜率为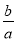 ;
;②
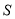 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.③当
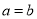 时,存在某个定点,该定点到
时,存在某个定点,该定点到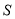 中的所有直线的距离均相等;
中的所有直线的距离均相等;④当
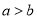 时,
时, 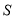 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为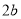 ;
;其中正确的是__________(写出所有正确命题的编号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
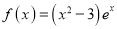 ,设关于
,设关于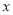 的方程
的方程 有
有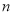 个不同的实数解,则
个不同的实数解,则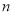 的所有可能的值为( )
的所有可能的值为( )A. 3 B. 1或3 C. 4或6 D. 3或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,以
为极点,以 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出曲线
 的直角坐标方程;
的直角坐标方程;(2)已知点
 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线
与曲线 相交于不同的两点
相交于不同的两点 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|ex﹣a|+|
 ﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
﹣1|,其中a,x∈R,e是自然对数的底数,e=2.71828…
(1)当a=0时,解不等式f(x)<2;
(2)求函数f(x)的单调增区间;
(3)设a≥ ,讨论关于x的方程f(f(x))=
,讨论关于x的方程f(f(x))=  的解的个数.
的解的个数.
相关试题

