【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() .设圆
.设圆![]() 的半径为1,圆心在
的半径为1,圆心在![]() 上.
上.
(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先联立两直线方程求得圆心坐标,然后设出切线方程,利用点到直线的距离求得切线斜率,从而求得切线的方程;(2)首先根据题条件设出圆的方程与点![]() 的坐标,然后根据
的坐标,然后根据![]() 得到
得到![]() 的轨迹方程,从而得出点
的轨迹方程,从而得出点![]() 应该既在圆
应该既在圆![]() 上又在圆
上又在圆![]() 上,且圆
上,且圆![]() 和圆
和圆![]() 有交点,进而确定不等关系式,求得
有交点,进而确定不等关系式,求得![]() 的取值范围.
的取值范围.
试题解析:(1)由题设,圆心![]() 是直线
是直线![]() 与直线
与直线![]() 的交点,
的交点,
由![]() ,解得
,解得![]() ,于是切线的斜率必存在.
,于是切线的斜率必存在.
设过![]() 的圆
的圆![]() 的切线方程为
的切线方程为![]() ,即
,即![]() ,
,
由题意,![]() ,解得
,解得![]() 或,或
或,或![]() .
.
故所求切线方程为![]() ,或
,或![]() ,即
,即![]() ,或
,或![]() .
.
(2)∵圆![]() 的圆心在直线
的圆心在直线![]() 上,
上,
∴圆![]() 的方程为
的方程为![]() ,
,
设点![]() ,由
,由![]() ,得
,得![]() ,
,
化简,得![]() ,即
,即![]() ,
,
∴点![]() 在以
在以![]() 为圆心,2为半径的圆上.
为圆心,2为半径的圆上.
由题意,点![]() 在圆
在圆![]() 上,
上,
∴圆![]() 和圆
和圆![]() 有公共点,则
有公共点,则![]() ,
,
∴![]() ,即
,即![]() .
.
由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() .
.
故圆心![]() 的横坐标
的横坐标![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:-1≤x<2,q:x<a,若q是p的必要条件,则a的取值范围是( )
A.a≤-1B.a≤-1或a≥2C.a≥2D.-1≤a<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
 /个
/个10
20
30
40
50
60
70
80
90
100
加工时间
 /分钟
/分钟62
68
75
81
89
95
102
108
115
122
(1)画出散点图,并判断
 与
与 是否具有线性相关关系;
是否具有线性相关关系;
(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,  .
.参考数据
合计

10
20
30
40
50
60
70
80
90
100
550

62
68
75
81
89
95
102
108
115
122
917

100
400
900
1600
2500
3600
4900
6400
8100
10000
38500

620
1360
2250
3240
4450
5700
7140
8840
10350
12200
55950
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
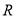 上的函数
上的函数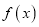 的导函数为
的导函数为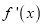 ,且满足
,且满足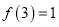 ,
, 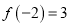 ,当
,当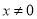 时有
时有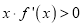 恒成立,若非负实数
恒成立,若非负实数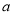 、
、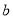 满足
满足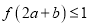 ,
, 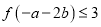 ,则
,则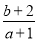 的取值范围为 .
的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设
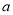 为非负实数,函数
为非负实数,函数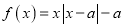 .
.(1)当
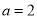 时,求
时,求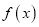 的单调区间;
的单调区间;(2)讨论函数
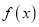 零点的个数,并求出零点.
零点的个数,并求出零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关,随机抽取了55名市民,得数据如下表:
喜欢
不喜欢
合计
男
20
5
25
女
10
20
30
合计
30
25
55
(1)判断是否有99.5%的把握认为喜欢观看体育节目与性别有关?
(2)用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求男市民人数
 的分布列和期望.
的分布列和期望.下面的临界值表供参考:

0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

