【题目】已知函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
(1)不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(2)设![]() 在
在![]() 内的实根为
内的实根为![]() ,
, 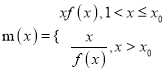 ,若在区间
,若在区间![]() 上存在
上存在![]() ,证明:
,证明: ![]() .
.
参考答案:
【答案】(1)1(2)见解析
【解析】试题分析:(1)不等式恒成立问题,一般利用变量分离,转化为对应函数最值问题,即![]() 的最小值,再利用导数求出函数
的最小值,再利用导数求出函数![]() 的最小值
的最小值![]() ,即得
,即得![]() ,因此实数
,因此实数![]() 的最大值为
的最大值为![]() .(2)先根据函数
.(2)先根据函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,求出
对称,求出![]() ,再由
,再由![]() 在
在![]() 内的实根为
内的实根为![]() ,得等量关系
,得等量关系![]() ,利用导数研究函数
,利用导数研究函数![]() 单调性:在
单调性:在![]() 上单调递增;在
上单调递增;在![]() 上单调递增减,因此
上单调递增减,因此![]() ,
, ![]() ,
, ![]() 为其极大值点,根据极点偏移方法证明
为其极大值点,根据极点偏移方法证明![]() :要证:
:要证: ![]() ,即证:
,即证: ![]() ,只要证
,只要证![]() ,即证
,即证![]() ,构造函数
,构造函数![]() ,其中
,其中![]() .利用导数可得
.利用导数可得![]() 在
在![]() 上单调递增,即得
上单调递增,即得![]()
试题解析:(1)由![]() ,所以
,所以![]() ,
,
设![]() ,∴
,∴![]() .
.
由![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,所以实数
,所以实数![]() 的最大值为
的最大值为![]() .
.
(2)设![]() 为函数
为函数![]() 图象上任意一点,
图象上任意一点,
则点![]() 为函数
为函数![]() 图象上的点,所以
图象上的点,所以![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,因而
,因而![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,因而
,因而![]() 在
在![]() 上单调递增减,
上单调递增减,
又![]() ,则
,则![]() ,
, ![]() ,
,
显然当![]() 时,
时, ![]() .
.
要证: ![]() ,即证:
,即证: ![]() ,而
,而![]() 在
在![]() 上单调递增减,
上单调递增减,
故可证![]() ,又由
,又由![]() ,即证
,即证![]() ,
,
即![]() ,
,
记![]() ,其中
,其中![]() .
.
![]() .
.
设![]() ,当
,当![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ,
,
故![]() .
.
而![]() ,故
,故![]() ,而
,而![]() ,从而
,从而![]() ,
,
因此当![]() ,即
,即![]() 单调递增.
单调递增.
从而当![]() 时,
时, ![]() ,即
,即![]() ,故
,故![]() 得证.
得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
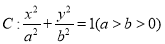 的左、右焦点分别为
的左、右焦点分别为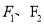 ,点
,点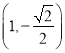 是椭圆
是椭圆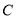 上的点,离心率
上的点,离心率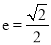 .
.(1)求椭圆
 的方程;
的方程;(2)点
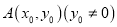 在椭圆
在椭圆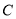 上,若点
上,若点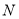 与点
与点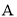 关于原点对称,连接
关于原点对称,连接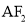 并延长与椭圆
并延长与椭圆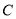 的另一个交点为
的另一个交点为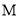 ,连接
,连接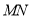 ,求
,求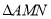 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中,an=32,sn=63,
(1)若数列{an}为公差为11的等差数列,求a1;
(2)若数列{an}为以a1=1为首项的等比数列,求数列{am2}的前m项和sm′ . -
科目: 来源: 题型:
查看答案和解析>>【题目】某颜料公司生产
 、
、 两种产品,其中生产每吨
两种产品,其中生产每吨 产品,需要甲染料
产品,需要甲染料 吨,乙染料
吨,乙染料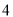 吨,丙染料
吨,丙染料 吨,生产每吨
吨,生产每吨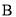 产品,需要甲染料
产品,需要甲染料 吨,乙染料
吨,乙染料 吨,丙染料
吨,丙染料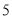 吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过
吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过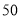 吨、
吨、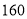 吨、
吨、 吨,如果
吨,如果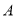 产品的利润为
产品的利润为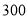 元/吨,
元/吨, 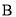 产品的利润为
产品的利润为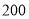 元/吨,则该颜料公司一天内可获得的最大利润为( )
元/吨,则该颜料公司一天内可获得的最大利润为( )A.
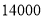 元 B.
元 B. 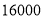 元 C.
元 C.  元 D.
元 D. 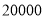 元
元 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在2060岁的问卷中随机抽取了100份, 统计结果如下面的图表所示.
年龄
分组
抽取份
数
答对全卷的人数
答对全卷的人数占本组的概率
[20,30)
40
28
0.7
[30,40)
n
27
0.9
[40,50)
10
4
b
[50,60]
20
a
0.1
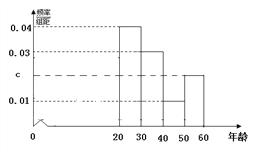
(1)分别求出n, a, b, c的值;
(2)从年龄在[40,60]答对全卷的人中随机抽取2人授予“环保之星”,求年龄在[50,60] 的人中至少有1人被授予“环保之星”的概率.
-
科目: 来源: 题型:
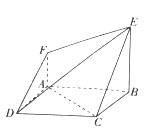
查看答案和解析>>【题目】如图所示的空间几何体中,底面四边形
 为正方形,
为正方形, 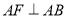 ,
,  ,平面
,平面 平面
平面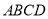 ,
, 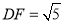 ,
, 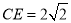 ,
, 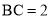 .
.
(1)求二面角
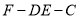 的大小;
的大小;(2)若在平面
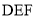 上存在点
上存在点 ,使得
,使得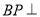 平面
平面 ,试通过计算说明点
,试通过计算说明点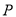 的位置.
的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知AB丄平面BCD,M、N分别是AC、AD的中点,BC 丄 CD.

(1)求证:MN//平面BCD;
(2)若AB=1,BC=
 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
相关试题

