【题目】如下图,在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,则直线D1E与A1D所成角的大小是 , 若D1E⊥EC,则直线A1D与平面D1DE所成的角为 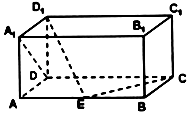
参考答案:
【答案】90°;30°
【解析】解:∵在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动,∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,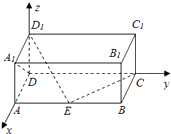
则D(0,0,0),D1(0,0,1),A(1,0,0),A1(1,0,1),C(0,2,0),
设E(1,t,0),0≤t≤2,
则 ![]() =(1,t,﹣1),
=(1,t,﹣1), ![]() =(﹣1,0,﹣1),
=(﹣1,0,﹣1),
∴ ![]()
![]() =﹣1+0+1=0,
=﹣1+0+1=0,
∴直线D1E与A1D所成角的大小是90°.
∵ ![]() =(1,t,﹣1),
=(1,t,﹣1), ![]() =(﹣1,2﹣t,0),D1E⊥EC,
=(﹣1,2﹣t,0),D1E⊥EC,
∴ ![]()
![]() =﹣1+t(2﹣t)+0=0,
=﹣1+t(2﹣t)+0=0,
解得t=1,∴AE=1.
平面D1DE的法向量为 ![]() =(﹣1,1,0),cos<
=(﹣1,1,0),cos< ![]() ,
, ![]() >=
>= ![]() =﹣
=﹣ ![]() ,
,
∴直线A1D与平面D1DE所成的角为30°.
所以答案是90°,30°.
【考点精析】本题主要考查了异面直线及其所成的角和空间角的异面直线所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则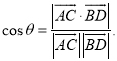 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C所对的边分别为a,b,c,已知sinA+sinC=psinB且
 .若角B为锐角,则p的取值范围是( )
.若角B为锐角,则p的取值范围是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为吸引顾客,某公司在商场举办电子游戏活动.对于
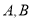 两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏
两种游戏,每种游戏玩一次均会出现两种结果,而且每次游戏的结果相互独立,具体规则如下:玩一次游戏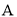 ,若绿灯闪亮,获得
,若绿灯闪亮,获得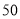 分,若绿灯不闪亮,则扣除
分,若绿灯不闪亮,则扣除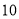 分(即获得
分(即获得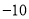 分),绿灯闪亮的概率为
分),绿灯闪亮的概率为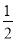 ;玩一次游戏
;玩一次游戏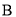 ,若出现音乐,获得
,若出现音乐,获得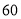 分,若没有出现音乐,则扣除
分,若没有出现音乐,则扣除 分(即获得
分(即获得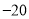 分),出现音乐的概率为
分),出现音乐的概率为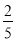 .玩多次游戏后累计积分达到
.玩多次游戏后累计积分达到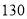 分可以兑换奖品.
分可以兑换奖品.(1)记
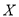 为玩游戏
为玩游戏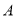 和
和 各一次所得的总分,求随机变量
各一次所得的总分,求随机变量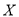 的分布列和数学期望;
的分布列和数学期望;(2)记某人玩
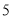 次游戏
次游戏 ,求该人能兑换奖品的概率.
,求该人能兑换奖品的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =f(2x)
=f(2x)
(1)用定义证明函数g(x)在(﹣∞,0)上为减函数.
(2)求g(x)在(﹣∞,﹣1]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+2x+b>0(a≠0)的解集为
 ,且a>b,则
,且a>b,则  的最小值是 .
的最小值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
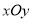 中,直线
中,直线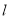 的参数方程为
的参数方程为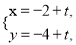 (
(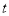 为参数).以原点
为参数).以原点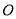 为极点,
为极点, 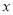 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线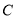 的极坐标方程为
的极坐标方程为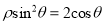 .直线
.直线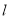 交曲线
交曲线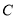 于
于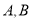 两点.
两点.(1)写出直线
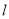 的极坐标方程和曲线
的极坐标方程和曲线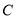 的直角坐标方程;
的直角坐标方程;(2)设点
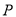 的直角坐标为
的直角坐标为 ,求点
,求点 到
到 两点的距离之积.
两点的距离之积.
相关试题

