【题目】如图,抛物线![]() 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆![]() 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为![]() ,
,![]() 在第一象限的交点为
在第一象限的交点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() 的面积为
的面积为![]() .
.
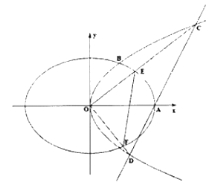
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
①求证:![]() 恒为钝角;
恒为钝角;
②射线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点,记
两点,记![]() 的面积分别是
的面积分别是![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)①证明见解析;② 存在,
;(2)①证明见解析;② 存在,![]() .
.
【解析】
试题分析:(1)由![]()
![]()
![]() .又
.又![]()
![]()
![]()
![]()
![]() .将点
.将点![]() 代入椭圆方程
代入椭圆方程![]()
![]()
![]() 椭圆为
椭圆为![]() ;(2)①设直线
;(2)①设直线![]() 的方程
的方程![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 恒为钝角;②
恒为钝角;②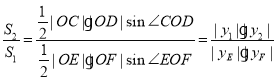 .由
.由![]() 的斜率为
的斜率为![]()
![]()
![]() :
:![]() .由
.由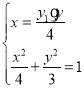
![]()
![]() 和
和![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 所求直线为
所求直线为![]() .
.
试题解析: (1)由![]() ,可得椭圆的长半轴
,可得椭圆的长半轴![]() .
.
∵![]() ,∴
,∴![]() ,代入抛物线求得
,代入抛物线求得![]() .
.
将点![]() 代入椭圆
代入椭圆![]() ,可得
,可得![]() ,
,
所以椭圆为![]() .
.
(2)①设直线![]() 的方程为
的方程为![]() ,由
,由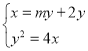 得
得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 恒为钝角;
恒为钝角;
②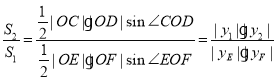 .
.
因为直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
由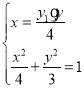 得
得![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
解之得:![]() ,所以所求直线为
,所以所求直线为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】由两点确定的直线中,斜率不存在的是
A.(4,2)与(-4,1) B.(0,3)与(3,0)
C.(3,-1)与(2, -1) D.(-2,2)与(-2,5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线y=2x2上一点A(2,8),则在点A处的切线斜率为 ( ).
A. 4 B. 16
C. 8 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某企业原有员工1000人,每人每年可为企业创利润15万元,为应对国际金融危机给企业带来的不利影响,该企业实施“优化重组,分流增效”的策略,分流出一部分员工待岗.为维护生产稳定,该企业决定待岗人数不超过原有员工的2%,并且每年给每位待岗员工发放生活补贴1万元.据评估,当待岗员工人数
 不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润
不超过原有员工1.4%时,留岗员工每人每年可为企业多创利润 万元;当待岗员工人数
万元;当待岗员工人数 超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.
超过原有员工1.4%时,留岗员工每人每年可为企业多创利润1.8万元.(1)求企业年利润
 (万元)关于待岗员工人数
(万元)关于待岗员工人数 的函数关系式
的函数关系式 ;
;(2)为使企业年利润最大,应安排多少员工待岗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与抛物线
与抛物线 交于
交于 两点,且线段
两点,且线段 恰好被点
恰好被点 平分.
平分.(1)求直线
 的方程;
的方程;(2)抛物线上是否存在点
 和
和 ,使得
,使得 关于直线
关于直线 对称?若存在,求出直线
对称?若存在,求出直线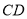 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线l过原点(0,0),且不过第三象限,那么l的倾斜角α的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,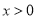 .
.(1)求
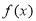 的极值;
的极值;(2)设
 ≤
≤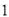 ,记
,记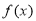 在
在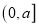 上的最大值为
上的最大值为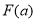 ,求函数
,求函数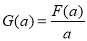 的最小值;
的最小值;(3)设函数
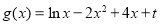 (
( 为常数),若使
为常数),若使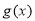 ≤
≤ ≤
≤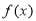 在
在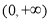 上恒成立的实数
上恒成立的实数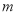 有且只有一个,求实数
有且只有一个,求实数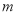 和
和 的值.
的值.
相关试题

