【题目】已知函数f(x)= ![]() .
.
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
参考答案:
【答案】
(1)解:任取x1,x2∈[1,+∞),且x1<x2,
f(x1)﹣f(x2)= ![]() =
= ![]() ,
,
∵x1﹣x2<0,(x1+1)(x2+1)>0,
所以f(x1)﹣f(x2)<0,即f(x1)<f(x2),
所以函数f(x)在[1,+∞)上是增函数
(2)解:由(1)知函数f(x)在[1,4]上是增函数,
∴最大值f(4)= ![]() ,最小值f(1)=
,最小值f(1)= ![]()
【解析】(1)根据增函数的定义进行判断和证明;(2)利用(1)的结论,利用函数的单调性.
【考点精析】关于本题考查的函数的值域和函数单调性的判断方法,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+
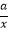 .
.
(1)判断f(x)的奇偶性并说明理由;
(2)当a=16时,判断f(x)在x∈(0,2]上的单调性并用定义证明;
(3)试判断方程x3﹣2016x+16=0在区间(0,+∞)上解的个数并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=2﹣x , g(x)=x﹣2
B.
C.
D.
-
科目: 来源: 题型:
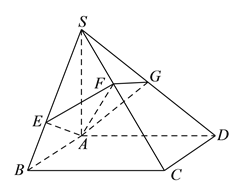
查看答案和解析>>【题目】如图,已知矩形
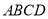 ,过
,过 作
作 平面
平面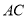 ,再过
,再过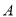 作
作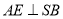 于点
于点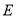 ,过
,过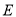 作
作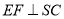 于点
于点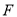 .
.(Ⅰ)求证:
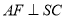 .
.(Ⅱ)若平面
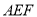 交
交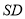 于点
于点 ,求证:
,求证: 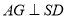 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公比为正数的等比数列,
是公比为正数的等比数列,  .
.(1)求
 的通项公式;
的通项公式;(2)设
 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和
的前n项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线
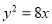 的焦点,斜率为
的焦点,斜率为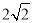 的直线交抛物线于
的直线交抛物线于 两点.
两点.(1)求线段
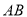 的长度;
的长度;(2)
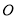 为坐标原点,
为坐标原点, 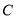 为抛物线上一点,若
为抛物线上一点,若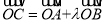 ,求
,求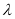 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
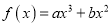 的图像经过点
的图像经过点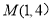 ,曲线
,曲线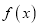 在点
在点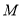 处的切线恰好与直线
处的切线恰好与直线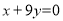 垂直.
垂直.(1)求实数
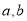 的值;
的值;(2)求在函数
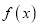 图像上任意一点处切线的斜率的取值范围.
图像上任意一点处切线的斜率的取值范围.
相关试题

