【题目】已知过抛物线![]() 的焦点,斜率为
的焦点,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点.
两点.
(1)求线段![]() 的长度;
的长度;
(2) ![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)9(2)λ=0或λ=2.
【解析】试题分析:第一问求抛物线的焦点弦长问题可直接利用焦半径公式,先写出直线的方程,再与抛物线的方程联立方程组,设而不求,利用根与系数关系得出![]() ,然后利用焦半径公式得出焦点弦长公式
,然后利用焦半径公式得出焦点弦长公式![]() ,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
试题解析:
(1)直线AB的方程是y=2![]() (x-2),与y2=8x联立,消去y得x2-5x+4=0,
(x-2),与y2=8x联立,消去y得x2-5x+4=0,
由根与系数的关系得x1+x2=5.由抛物线定义得|AB|=x1+x2+p=9,
(2)由x2-5x+4=0,得x1=1,x2=4,从而A(1,-2![]() ),B(4,4
),B(4,4![]() ).
).
设![]() =(x3,y3)=(1,-2
=(x3,y3)=(1,-2![]() )+λ(4,4
)+λ(4,4![]() )=(4λ+1,4
)=(4λ+1,4![]() λ-2
λ-2![]() ),
),
又y=8x3,即[2![]() (2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
解得λ=0或λ=2.
-
科目: 来源: 题型:
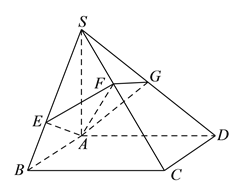
查看答案和解析>>【题目】如图,已知矩形
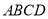 ,过
,过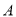 作
作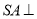 平面
平面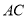 ,再过
,再过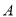 作
作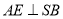 于点
于点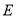 ,过
,过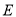 作
作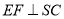 于点
于点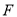 .
.(Ⅰ)求证:
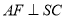 .
.(Ⅱ)若平面
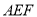 交
交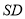 于点
于点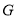 ,求证:
,求证: 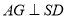 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
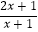 .
.
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是公比为正数的等比数列,
是公比为正数的等比数列,  .
.(1)求
 的通项公式;
的通项公式;(2)设
 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前n项和
的前n项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
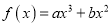 的图像经过点
的图像经过点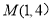 ,曲线
,曲线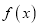 在点
在点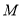 处的切线恰好与直线
处的切线恰好与直线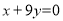 垂直.
垂直.(1)求实数
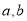 的值;
的值;(2)求在函数
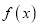 图像上任意一点处切线的斜率的取值范围.
图像上任意一点处切线的斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
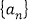 的前
的前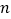 项和为
项和为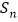 ,且
,且 成等差数列,
成等差数列,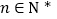 ,
, ,函数
,函数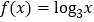 .
.(1)求数列
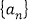 的通项公式;
的通项公式;(2)设数列
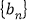 满足
满足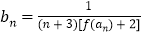 ,记数列
,记数列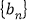 的前
的前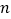 项和为
项和为 ,试比较
,试比较 与
与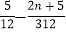 的大小?
的大小? -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)
 (单位:万件)与年促销费用
(单位:万件)与年促销费用 (单位:万元)(
(单位:万元)( )满足
)满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2017年该产品的利润
 (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用 (单位:万元)的函数;
(单位:万元)的函数;(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
相关试题

