【题目】盒子里装有4张卡片,上面分别写着数字1,1,2,2,每张卡片被取到的概率相等.先从盒子中任取1张卡片,记下上面的数字![]() ,然后放回盒子内搅匀,再从盒子中随机任取1张卡片,记下它上面的数字
,然后放回盒子内搅匀,再从盒子中随机任取1张卡片,记下它上面的数字![]() .
.
(1)求![]() 的概率
的概率![]() ;
;
(2)设“函数![]() 在区间
在区间![]() 内有且只有一个零点”为事件
内有且只有一个零点”为事件![]() ,求
,求![]() 的概率
的概率![]() .
.
参考答案:
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)利用列表法和古典概型的概率公式可求得结果;
(2)因为![]() 的值只能取
的值只能取![]() ,
,![]() ,
,![]() ,分别当
,分别当![]() 取2,3,4时,求出函数
取2,3,4时,求出函数![]() 的零点,可知只有
的零点,可知只有![]() 符合要求,然后求出
符合要求,然后求出![]() 的概率即可得到答案.
的概率即可得到答案.
(1)先后两次取到卡片的情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
共有16种情况. 满足![]() 的共有4种情况.
的共有4种情况.
所以![]() 的概率
的概率![]() .
.
(2)因为![]() 的值只能取
的值只能取![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]()
![]()
![]() 无解,所以
无解,所以![]() 没有零点,不符合要求.
没有零点,不符合要求.
当![]() 时,由
时,由![]()
![]()
![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 的零点分别为
的零点分别为![]() ,
,![]() ,所以
,所以![]() 在区间
在区间![]() 内只有
内只有![]() 这个零点,符合要求.
这个零点,符合要求.
当![]() 时,由
时,由![]()
![]()
![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() 的零点分别为
的零点分别为![]() ,
,![]() ,都不在区间
,都不在区间![]() 内,不符合要求.
内,不符合要求.
所以事件![]() 相当于
相当于![]() ,
,
由(1)知:满足![]() 的共有8种情况,所以
的共有8种情况,所以![]() .
.
即函数函数![]()
![]()
![]() 在区间
在区间![]() 内有且只有一个零点的概率等于
内有且只有一个零点的概率等于![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有
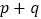 个零件,已知其中有
个零件,已知其中有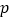 个正品、
个正品、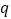 个次品.现随机地逐一检查,则恰好在检查第
个次品.现随机地逐一检查,则恰好在检查第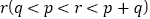 个零件查出了所有次品的概率为( ).
个零件查出了所有次品的概率为( ).A.
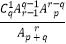 B.
B. 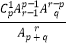
C.
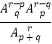 D.
D. 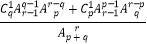
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点
的焦点 恰好是双曲线
恰好是双曲线 的一个焦点,且两条曲线交点的连线过点
的一个焦点,且两条曲线交点的连线过点 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )A.
 B.
B. C.
C. D.
D.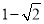
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 满足
满足 ,
,  .
.(1)求
 的通项公式;
的通项公式; (2)各项均为正数的等比数列
 中,
中,  ,
,  ,求
,求 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
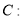
 的右顶点
的右顶点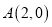 ,离心率为
,离心率为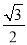 ,
, 为坐标原点.
为坐标原点.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)已知
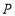 (异于点
(异于点 )为椭圆
)为椭圆 上一个动点,过
上一个动点,过 作线段
作线段 的垂线
的垂线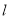 交椭圆
交椭圆 于点
于点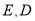 ,求
,求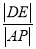 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+
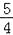 }是等比数列.
}是等比数列. -
科目: 来源: 题型:
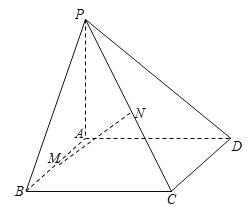
查看答案和解析>>【题目】已知矩形
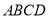 ,
,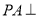 面
面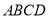 ,
,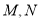 分别是
分别是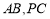 的中点,设
的中点,设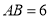 ,
,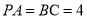 .
.
(1)证明:
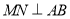 ;
;(2)求二面角
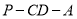 的大小.
的大小.
相关试题

