【题目】一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
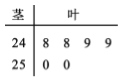
(Ⅰ)求这箱饮料的平均容量和容量的中位数;
(Ⅱ)如果从这箱饮料中随机取出2听饮用,求取到的2听饮料中至少有1听的容量为250ml的概率
参考答案:
【答案】(Ⅰ)根据平均数计算公式得饮料的平均容量为![]() ,中位数为中间两个数的平均值:
,中位数为中间两个数的平均值:![]() (Ⅱ)先利用枚举法确定从这6听饮料中随机抽取2听的所有可能结果,共有15种,其中取到的2听饮料容量都不为250ml的种数有6种,因此取到的2听饮料中至少有1听的容量为250ml的有9种,故根据古典概型概率公式得
(Ⅱ)先利用枚举法确定从这6听饮料中随机抽取2听的所有可能结果,共有15种,其中取到的2听饮料容量都不为250ml的种数有6种,因此取到的2听饮料中至少有1听的容量为250ml的有9种,故根据古典概型概率公式得![]()
【解析】
试题分析:(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
试题解析:(Ⅰ)由茎叶图知,这箱饮料的平均容量为![]() .
.
容量的中位数为![]() .…………………………………………4分
.…………………………………………4分
(Ⅱ)把每听饮料标上号码,其中容量为248ml,249ml的4听分别记作:1,2,3,4,容量为250ml的2听分别记作:![]() ,
,![]() .抽取2听饮料,得到的两个标记分别记为
.抽取2听饮料,得到的两个标记分别记为![]() 和
和![]() ,则
,则![]() 表示一次抽取的结果,即基本事件,从这6听饮料中随机抽取2听的所有可能结果有:
表示一次抽取的结果,即基本事件,从这6听饮料中随机抽取2听的所有可能结果有:
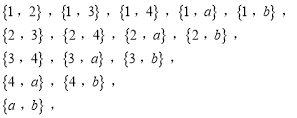
共计15种,即事件总数为15.
其中含有![]() 或
或![]() 的抽取结果恰有9种,即“随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml”的基本事件个数为9.
的抽取结果恰有9种,即“随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml”的基本事件个数为9.
所以从这箱饮料中随机取出2听饮用,取到的2听饮料中至少有1听的容量为250ml的概率为![]() .……12分
.……12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,设
,设 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)由
 的图象经过怎样变换得到
的图象经过怎样变换得到 的图象?试写出变换过程;
的图象?试写出变换过程;(3)当
 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有10道题,其中6道甲类题,4道乙类题,小明同学从中任取3道题解答.
(Ⅰ)求小明同学至少取到1道乙类题的概率;
(Ⅱ)已知所取的3道题中有2道甲类题,1道乙类题.若小明同学答对每道甲类题的概率都是
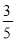 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是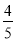 ,且各题答对与否相互独立.求小明同学至少答对2道题的概率.
,且各题答对与否相互独立.求小明同学至少答对2道题的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在对人们休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2列联表;
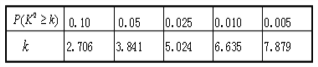
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为性别与休闲方式有关系?
附:
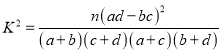
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
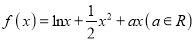 ,
, 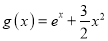 .
.(Ⅰ)讨论
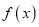 的极值点的个数;
的极值点的个数;(Ⅱ)若对于任意
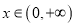 ,总有
,总有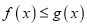 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是两条不同的直线,
是两条不同的直线,  是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: ①若
 ,则
,则 ②若
②若 ,则
,则
③若
 ,则
,则 ④若
④若 ,则
,则
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区某种农产品的年产量
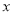 (单位:吨)对价格
(单位:吨)对价格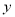 (单位:千元/吨)和利润
(单位:千元/吨)和利润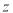 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:
(1)求
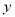 关于
关于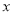 的线性回归方程;
的线性回归方程;(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润
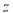 取到最大值?(结果保留两位小数)
取到最大值?(结果保留两位小数)参考公式:
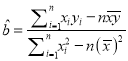 ,
, 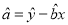
参考数据:
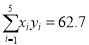 ,
, 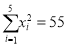 .
.
相关试题

