【题目】已知椭圆x2+![]() =1(0<b<1)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C三点作圆P,其中圆心P的坐标为(m,n).
=1(0<b<1)的左焦点为F,左、右顶点分别为A、C,上顶点为B,过F、B、C三点作圆P,其中圆心P的坐标为(m,n).
(1)若FC是圆P的直径,求椭圆的离心率;
(2)若圆P的圆心在直线x+y=0上,求椭圆的方程.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】【试题分析】(1)根据椭圆的性质得出![]() 点的坐标,利用直径所对圆周角是直角,即
点的坐标,利用直径所对圆周角是直角,即![]() .列方程解出
.列方程解出![]() 的值,由此求得离心率.(2)求得直线
的值,由此求得离心率.(2)求得直线![]() 和
和![]() 垂直平分线的方程,求得
垂直平分线的方程,求得![]() 的值,代入直线方程可求得
的值,代入直线方程可求得![]() ,由此解得
,由此解得![]() 的值并求出椭圆方程.
的值并求出椭圆方程.
【试题解析】
(1)由椭圆的方程知a=1,
点B(0,b),C(1,0).设F的坐标为(-c,0)(c>0),
∵FC是圆P的直径,
∴FB⊥BC,
∵kBC=-b,kBF=![]() ,
,
∴-b·![]() =-1,
=-1,
∴b2=c=1-c2,c2+c-1=0,
解得c=![]() ,∴椭圆的离心率e=
,∴椭圆的离心率e=![]() =
=![]() .
.
(2)∵圆P过F、B、C三点,
∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,
FC的垂直平分线方程为x=![]() ,①
,①
∵BC的中点为![]() ,kBC=-b,
,kBC=-b,
∴BC的垂直平分线方程为y-![]() =
=![]()
![]() ,②
,②
由①②得x=![]() ,y=
,y=![]() ,
,
即m=![]() ,n=
,n=![]() .
.
∵P(m,n)在直线x+y=0上,
∴![]() +
+![]() =0(1+b)(b-c)=0.
=0(1+b)(b-c)=0.
∵1+b>0,
∴b=c.
由b2=1-c2得b2=![]() ,
,
∴椭圆的方程为x2+![]() =1.
=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线y=x+ln x在点(1,1)处的切线与曲线y=ax2+(a+2)x+1相切,则a=________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱台ABCD﹣A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=2AD,AD=A1B1,∠BAD=60°.
(Ⅰ)证明:CC1∥平面A1BD;
(Ⅱ)求直线CC1与平面ADD1A1所成角的正弦值

-
科目: 来源: 题型:
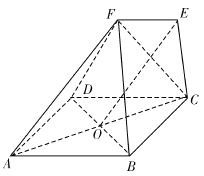
查看答案和解析>>【题目】如图,在几何体中,四边形
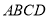 为菱形,对角线
为菱形,对角线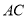 与
与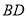 的交点为
的交点为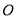 ,四边形
,四边形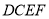 为梯形,
为梯形, 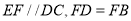 .
.
(Ⅰ)若
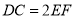 ,求证:
,求证: 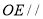 平面
平面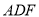 ;
;(Ⅱ)求证:平面
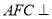 平面
平面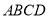 ;
;(Ⅲ)若
 ,
, 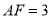 ,
, 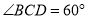 ,求
,求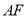 与平面
与平面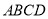 所成角.
所成角. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
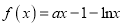 .(
.(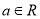 )
)(Ⅰ)讨论函数
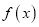 的单调性;
的单调性;(Ⅱ)若函数
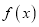 在x=2处的切线斜率为
在x=2处的切线斜率为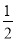 ,不等式
,不等式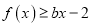 对任意
对任意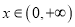 恒成立,求实数
恒成立,求实数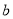 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
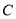 :
: 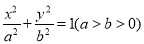 的左、右焦点分别为
的左、右焦点分别为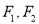 ,上顶点为
,上顶点为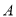 ,过点
,过点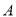 与
与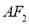 垂直的直线交
垂直的直线交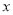 轴负半轴于点
轴负半轴于点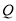 ,且
,且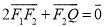 .
. (Ⅰ)求椭圆
 的离心率;
的离心率;(Ⅱ)若过
 、
、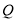 、
、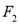 三点的圆恰好与直线
三点的圆恰好与直线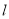 :
: 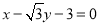 相切,求椭圆
相切,求椭圆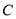 的方程;
的方程;(III)在(Ⅱ)的条件下,过右焦点
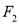 作斜率为
作斜率为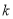 的直线
的直线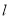 与椭圆
与椭圆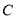 交于
交于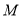 、
、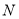 两点,在
两点,在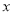 轴上是否存在点
轴上是否存在点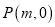 使得以
使得以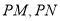 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出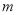 的取值范围,如果不存在,说明理由
的取值范围,如果不存在,说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=aln x+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数f(x)的解析式及单调区间;
(2)若函数g(x)=f(x)+m-ln 4在
 上恰有两个零点,求实数m的取值范围.
上恰有两个零点,求实数m的取值范围.
相关试题

